题目内容
1.如图1,在平面直角坐标系中,OA=OB=OC,以O为圆心,3为半径作⊙O刚好与AC相切于D.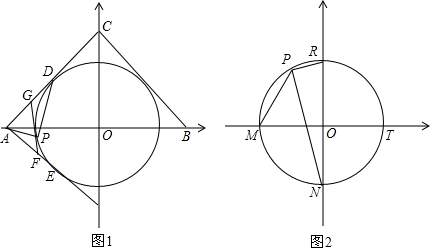
(1)求证:BC与⊙O相切.
(2)若AE切⊙O于E,P为弧DE上一点,过P作⊙O的切线,分别交AC、AE于G、F两点,连PA、PD,且满足GA=$\frac{3}{4}$AF.求证:PA⊥PD.
(3)如图2,若⊙O交坐标轴于M、N、T、R,点P为弧MR上任一点,连MP、PR、PN.现给出两个结论①$\frac{PN-PR}{PM}$为定值;②PN-PR为定值.其中只有一个结论正确,请选择正确的结论证明并求值.
分析 (1)过点O作OH⊥BC,连接OD,如图1,要证BC与⊙O相切,只需证OH=OD即可;
(2)连接OE,如图1,易证四边形ODAE是正方形,则有AD=AE=OD=3.设AF=4x,则GA=$\frac{3}{4}$AF=3x,根据勾股定理可得GF=5x,根据切线长定理可得GD=GP,FP=FE,由此可得到AD+AE=12x=6,即可得到x=$\frac{1}{2}$,从而可得到AG=DG=GP=$\frac{3}{2}$,由此可证到PA⊥PD;
(3)连接PO并延长交⊙O于Q,连接MQ交PN于S,连接NQ,如图2,根据圆周角定理可得∠MPN=$\frac{1}{2}$∠MON=45°,∠PMQ=∠PNQ=90°,即可得到∠PSM=∠NSQ=∠SQN=45°,从而可得到PS=$\sqrt{2}$PM,NS=NQ.由∠POR=∠NOQ可得到PR=NQ,则有PR=NS,从而可得PN-PR=PN-NS=PS=$\sqrt{2}$PM,即可得到$\frac{PN-PR}{PM}$=$\sqrt{2}$(定值),PN-PR随点P的变化而变化,不是定值.
解答 证明:(1)过点O作OH⊥BC,连接OD,如图1,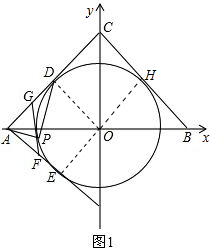
则有OD⊥AC.
∵OA=OB=OC,∠AOC=∠BOC=90°,
∴∠CAO=∠ACO=∠BCO=45°,
∴OH=OD,
∴BC与⊙O相切;
(2)连接OE,如图1,
则有OE⊥AE.
∵OD⊥AC,OE⊥AE,OD=OE,
∴∠EAO=∠DAO=45°,
∴∠DAE=90°,
∴∠ODA=∠DAE=∠AEO=90°,
∴四边形ODAE是矩形.
∵OD=OE,
∴矩形ODAE是正方形,
∴AD=AE=OD=3.
设AF=4x,则GA=$\frac{3}{4}$AF=3x,
∴GF=5x.
∵GF、GD、EF都是⊙O的切线,
∴GD=GP,FP=FE,
∴AD+AE=AG+GF+AF=12x=6,
∴x=$\frac{1}{2}$,
∴AG=$\frac{3}{2}$,
∴GP=GD=3-$\frac{3}{2}$=$\frac{3}{2}$=AG,
∴∠PAG=∠PGA.
∵GD=GP,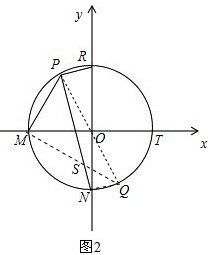
∴∠GPD=∠GDP.
∵∠GAF+∠APG+∠GPD+∠GDP=180°,
∴2∠APG+2∠GPD=180°,
∴∠APD=90°即AP⊥DP;
(3)结论①正确,结论②错误.
证明:连接PO并延长,交⊙O于Q,连接MQ交PN于S,连接NQ,如图2.
则∠MPN=$\frac{1}{2}$∠MON=45°,∠PMQ=∠PNQ=90°,
∴∠PSM=45°,∠NSQ=45°=∠SQN,
∴PS=$\sqrt{2}$PM,NS=NQ.
∵∠POR=∠NOQ,∴PR=NQ,
∴PR=NS,
∴PN-PR=PN-NS=PS=$\sqrt{2}$PM,
∴$\frac{PN-PR}{PM}$=$\sqrt{2}$(定值).
∵点P为弧MR上任一点,
∴PM随着点P的变化而变化,
∴PN-PR随着点P的变化而变化.
点评 本题主要考查了切线的判定与性质、切线长定理、圆周角定理、正方形的判定与性质、圆心角与弦的关系、等腰直角三角形的性质、勾股定理等知识,证到AG=DG=GP是解决第(2)小题,把PN-PR转化为PS是解决第(3)小题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | (a+b)2=a2+b2 | B. | (x+6)(x-6)=x2-6 | C. | (x+2)2=x2+2x+4 | D. | (x-y)2=(y-x)2 |
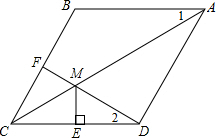 已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.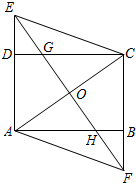 如图,已知在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E、F,交边DC于点G,交边AB于点H.联结AF,CE.
如图,已知在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E、F,交边DC于点G,交边AB于点H.联结AF,CE. 如图,点D、E分别在AB、BC上,DE∥AC,AF∥BC,∠1=60°,则∠2=60°.
如图,点D、E分别在AB、BC上,DE∥AC,AF∥BC,∠1=60°,则∠2=60°.