题目内容
6. 如图,如果一个直角三角形的内接正方形的面积恰好是三角形面积的0.48倍,则该直角三角形的两条直角边的比为( )
如图,如果一个直角三角形的内接正方形的面积恰好是三角形面积的0.48倍,则该直角三角形的两条直角边的比为( )| A. | 1:2 | B. | 2:3 | C. | 3:4 | D. | 4:5 |
分析 根据正方形的性质可得出∠AFE=∠EDC=90°、∠AEF=∠ECD,由此即可得出△AEF∽△ECD,根据相似三角形的性质可得出$\frac{EF}{CD}=\frac{AF}{DE}$,设AB=a,BC=b,DE=EF=c,则AF=a-c,CD=b-c,结合$\frac{EF}{CD}=\frac{AF}{DE}$以及S正方形BDEF=0.48S△ABC,即可得出关于$\frac{b}{a}$的一元二次方程,解方程即可得出结论.
解答 解:在图中标上字母,如图所示.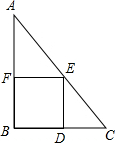
∵四边形BDEF为正方形,
∴∠BFE=∠BDE=90°,EF∥BD,
∴∠AFE=∠EDC=90°,∠AEF=∠ECD,
∴△AEF∽△ECD,
∴$\frac{EF}{CD}=\frac{AF}{DE}$.
设AB=a,BC=b,DE=EF=c,则AF=a-c,CD=b-c,
∴c2=(a-c)(b-c),
∴c=$\frac{ab}{a+b}$.
∵S正方形BDEF=0.48S△ABC,
∴c2=0.24ab=$(\frac{ab}{a+b})^{2}$,
∴6•$(\frac{b}{a})^{2}$-13•$\frac{b}{a}$+6=0,
解得:$\frac{b}{a}$=$\frac{2}{3}$或$\frac{b}{a}$=$\frac{3}{2}$,
∴该直角三角形的两条直角边的比为2:3.
故选B.
点评 本题考查了相似三角形的判定与性质,解题的关键是得出关于$\frac{b}{a}$的一元二次方程.本题属于中档题,难度不大,解决该题型题目时,根据相似三角形的性质找出边与边的关系是关键.

练习册系列答案
相关题目
16.下面与-3乘积为1的数是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
17. 如图,在四边形ABCD中,点E,F,G分别是边AB,AD,DC的中点,则EF=( )
如图,在四边形ABCD中,点E,F,G分别是边AB,AD,DC的中点,则EF=( )
 如图,在四边形ABCD中,点E,F,G分别是边AB,AD,DC的中点,则EF=( )
如图,在四边形ABCD中,点E,F,G分别是边AB,AD,DC的中点,则EF=( )| A. | $\frac{1}{3}$BD | B. | $\frac{1}{2}$BD | C. | $\frac{1}{2}$BG | D. | BG |
1.11+101+1001+…+$\underset{\underbrace{10…01}}{99个0}$的和为( )
| A. | $\underset{\underbrace{11…1210}}{98个1}$ | B. | $\underset{\underbrace{11…1210}}{99个1}$ | C. | $\underset{\underbrace{11…10}}{100个1}$ | D. | $\underset{\underbrace{11…10}}{101个1}$ |
11.函数y=x|x|-3x+1的图象与x轴交点的个数为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 0 |
18.按如图的运算程序,能使输出结果为3的x,y的值是( )


| A. | x=5,y=-2 | B. | x=3,y=-3 | C. | x=-4,y=2 | D. | x=-3,y=-9 |

 二次函数y=x2+(2m+1)x+m2的图象交x轴于A(x1,0)、B(x2,0),已知x1<x2且x12+x1•x2+x22=21.
二次函数y=x2+(2m+1)x+m2的图象交x轴于A(x1,0)、B(x2,0),已知x1<x2且x12+x1•x2+x22=21.