题目内容
13.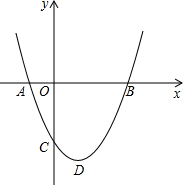 如图,二次函数y=ax2+bx+c图象的顶点D的横坐标为1,其图象与x轴的交点为A、B,3<AB<4,则|a-b+c|+|2a+b+c|=( )
如图,二次函数y=ax2+bx+c图象的顶点D的横坐标为1,其图象与x轴的交点为A、B,3<AB<4,则|a-b+c|+|2a+b+c|=( )| A. | a-b | B. | 3a+2c | C. | a+2b | D. | -a-b |
分析 根据二次函数开口向上确定出a>0,根据函数图象与y轴的交点确定出c<0,根据顶点的横坐标确定出b,再根据AB的长度求出点A的横坐标的取值范围,从而确定出横坐标为-1的点在第二象限,然后求出a-b+c>0,最后根据绝对值的性质去掉绝对值号,然后进行整式的加减即可.
解答 解:∵二次函数开口向上,
∴a>0,
∵函数图象与y轴负半轴相交,
∴c<0,
∵顶点D的横坐标为1,
∴-$\frac{b}{2a}$=1,
∴b=-2a,
∴2a+b=0,
∵3<AB<4,
∴1.5<$\frac{1}{2}$AB<2,
∵点D的横坐标是1,
∴-1<点A的横坐标<0,
∴横坐标为-1的点在第二象限,
当x=-1时,a-b+c>0,
∴|a-b+c|+|2a+b+c|=a-b+c-c=a-b.
故选A.
点评 本题考查了二次函数图象与系数的关系,绝对值的性质,熟练掌握二次函数的性质是解题的关键,本题难点在于确定出横坐标为-1的点所在的象限.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
3.已知一组数据:12,5,9,5,14,下列说法不正确的是( )
| A. | 平均数是9 | B. | 中位数是9 | C. | 众数是5 | D. | 极差是5 |
4.某种电子元件的面积大约为0.00000069平方毫米,将0.00000069这个数用科学记数法表示正确的是( )
| A. | 0.69×10-6 | B. | 6.9×10-7 | C. | 69×10-8 | D. | 6.9×107 |
1. 小明将图中两水平线l1与l2的其中一条当成x轴,且向右为正方向;两铅垂线l3与l4的其中一条当成y轴,且向上为正方向,并且在此平面直角坐标系上画出二次函数y=-x2-2x+1的图象,则关于他选择x轴与y轴的叙述正确的是( )
小明将图中两水平线l1与l2的其中一条当成x轴,且向右为正方向;两铅垂线l3与l4的其中一条当成y轴,且向上为正方向,并且在此平面直角坐标系上画出二次函数y=-x2-2x+1的图象,则关于他选择x轴与y轴的叙述正确的是( )
 小明将图中两水平线l1与l2的其中一条当成x轴,且向右为正方向;两铅垂线l3与l4的其中一条当成y轴,且向上为正方向,并且在此平面直角坐标系上画出二次函数y=-x2-2x+1的图象,则关于他选择x轴与y轴的叙述正确的是( )
小明将图中两水平线l1与l2的其中一条当成x轴,且向右为正方向;两铅垂线l3与l4的其中一条当成y轴,且向上为正方向,并且在此平面直角坐标系上画出二次函数y=-x2-2x+1的图象,则关于他选择x轴与y轴的叙述正确的是( )| A. | l1为x轴,l3为y轴 | B. | l1为x轴,l4为y轴 | C. | l2为x轴,l3为y轴 | D. | l2为x轴,l4为y轴 |
2.已知一组数据:2,3,3,5,7,下列说法不正确的是( )
| A. | 平均数是4 | B. | 中位数是5 | C. | 众数是3 | D. | 方差是3.2 |
3.已知二次函数y=x2-2mx(m为常数),当-1≤x≤2时,函数值y的最小值为-2,则m的值是( )
| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$或$\sqrt{2}$ | D. | $-\frac{3}{2}$或$\sqrt{2}$ |
 如图,⊙O的半径为3,弦AB与弦CD平行,将图中阴影部分沿直线CD折叠后所得圆弧恰与AB相切.若CD=2$\sqrt{5}$,则AB=4$\sqrt{2}$.
如图,⊙O的半径为3,弦AB与弦CD平行,将图中阴影部分沿直线CD折叠后所得圆弧恰与AB相切.若CD=2$\sqrt{5}$,则AB=4$\sqrt{2}$.