题目内容
18. 如图,⊙O的半径为3,弦AB与弦CD平行,将图中阴影部分沿直线CD折叠后所得圆弧恰与AB相切.若CD=2$\sqrt{5}$,则AB=4$\sqrt{2}$.
如图,⊙O的半径为3,弦AB与弦CD平行,将图中阴影部分沿直线CD折叠后所得圆弧恰与AB相切.若CD=2$\sqrt{5}$,则AB=4$\sqrt{2}$.
分析 连接OB、OD,作OH⊥CD于H交⊙O于M,交AB于N.分别在Rt△ODH,Rt△OBN中,解直角三角形即可.
解答 解:连接OB、OD,作OH⊥CD于H交⊙O于M,交AB于N.
∵OH⊥CD,
∴CH=HD=$\sqrt{5}$,
在Rt△ODH中,OH=$\sqrt{O{D}^{2}-D{H}^{2}}$=2,
∴HM=HN=3-2=1,ON=3-2=1,
在Rt△OBN中,BN=$\sqrt{O{B}^{2}-O{N}^{2}}$=$\sqrt{9-1}$=2$\sqrt{2}$,
∵AB∥CD,ON⊥CD,
∴ON⊥AB,
∴AN=BN=2$\sqrt{2}$,
∴AB=4$\sqrt{2}$.
故答案为4$\sqrt{2}$.
点评 本题考查切线的性质、垂径定理、翻折变换、解直角三角形、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
8.如图,数轴的单位长度为1,点A,B表示的两个数互为相反数,点A表示的数是( )


| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
6.在平面直角坐标系中,点A的坐标是(-1,0),点B的坐标是(3,0),在y轴的正半轴上取一点C,使A、B、C三点确定一个圆,且使AB为圆的直径,则点C的坐标是( )
| A. | (0,$\sqrt{3}$) | B. | ($\sqrt{3}$,0) | C. | (0,2) | D. | (2,0) |
13.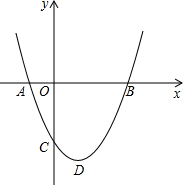 如图,二次函数y=ax2+bx+c图象的顶点D的横坐标为1,其图象与x轴的交点为A、B,3<AB<4,则|a-b+c|+|2a+b+c|=( )
如图,二次函数y=ax2+bx+c图象的顶点D的横坐标为1,其图象与x轴的交点为A、B,3<AB<4,则|a-b+c|+|2a+b+c|=( )
 如图,二次函数y=ax2+bx+c图象的顶点D的横坐标为1,其图象与x轴的交点为A、B,3<AB<4,则|a-b+c|+|2a+b+c|=( )
如图,二次函数y=ax2+bx+c图象的顶点D的横坐标为1,其图象与x轴的交点为A、B,3<AB<4,则|a-b+c|+|2a+b+c|=( )| A. | a-b | B. | 3a+2c | C. | a+2b | D. | -a-b |
3.若x<y,则下列式子中正确的是( )
| A. | mx<my | B. | x+m<y+m | C. | -$\frac{x}{m}$<-$\frac{y}{m}$ | D. | mx2<my2 |
10. 如图,用直尺和三角尺画图:已知点P和直线a,经过点P作直线b,使b∥a,其画法的依据是( )
如图,用直尺和三角尺画图:已知点P和直线a,经过点P作直线b,使b∥a,其画法的依据是( )
 如图,用直尺和三角尺画图:已知点P和直线a,经过点P作直线b,使b∥a,其画法的依据是( )
如图,用直尺和三角尺画图:已知点P和直线a,经过点P作直线b,使b∥a,其画法的依据是( )| A. | 同位角相等,两直线平行 | |
| B. | 两直线平行,同位角相等 | |
| C. | 过直线外一点有且只有一条直线与已知直线平行 | |
| D. | 内错角相等,两直线平行 |
8.作为世界文化遗产的长城,其总长大约为6700000m.将6700000用科学记数法表示为( )
| A. | 6.7×105 | B. | 6.7×106 | C. | 0.67×107 | D. | 67×108 |
 已知:如图,直线a⊥m,直线b⊥m,若∠1=60°,则∠2的度数是120°.
已知:如图,直线a⊥m,直线b⊥m,若∠1=60°,则∠2的度数是120°.