题目内容
1．
小明将图中两水平线l1与l2的其中一条当成x轴，且向右为正方向；两铅垂线l3与l4的其中一条当成y轴，且向上为正方向，并且在此平面直角坐标系上画出二次函数y=-x2-2x+1的图象，则关于他选择x轴与y轴的叙述正确的是（ ）| A． | l1为x轴，l3为y轴 | B． | l1为x轴，l4为y轴 | C． | l2为x轴，l3为y轴 | D． | l2为x轴，l4为y轴 |
分析 首先求出二次函数的对称轴以及顶点坐标，进而得出x轴与y轴的位置．
解答 解：y=-x2-2x+1
=-（x+1）2+2，
故抛物线的对称轴为：直线x=-1，顶点坐标为：（-1，2），
则关于他选择x轴与y轴的叙述正确的是：l2为x轴，l4为y轴．
故选：D．
点评 此题主要考查了二次函数的图象，正确求出二次函数的对称轴与顶点坐标是解题关键．
练习册系列答案
相关题目
11．
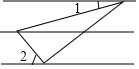如图，小明把一块含有60°锐角的直角三角板的三个顶点分别放在一组平行线上，如果∠1=20°，那么∠2的度数是（ ）
如图，小明把一块含有60°锐角的直角三角板的三个顶点分别放在一组平行线上，如果∠1=20°，那么∠2的度数是（ ）| A． | 25° | B． | 30° | C． | 40° | D． | 45° |
12．7的相反数是（ ）
| A． | -7 | B． | -$\frac{4}{7}$ | C． | $\frac{1}{7}$ | D． | 7 |
已知：如图，直线a⊥m，直线b⊥m，若∠1=60°，则∠2的度数是120°．
16．一家鞋店在一段时间内销售某种女鞋50双，各种尺码的销售量如表所示：
如果你是店长，为了增加销售量，你最关注哪个统计量（ ）
| 尺码（厘米） | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 销售量（双） | 1 | 2 | 31 | 5 | 7 | 3 | 1 |
| A． | 平均数 | B． | 众数 | C． | 中位数 | D． | 方差 |
6．在平面直角坐标系中，点A的坐标是（-1，0），点B的坐标是（3，0），在y轴的正半轴上取一点C，使A、B、C三点确定一个圆，且使AB为圆的直径，则点C的坐标是（ ）
| A． | （0，$\sqrt{3}$） | B． | （$\sqrt{3}$，0） | C． | （0，2） | D． | （2，0） |
13．
如图，二次函数y=ax2+bx+c图象的顶点D的横坐标为1，其图象与x轴的交点为A、B，3＜AB＜4，则|a-b+c|+|2a+b+c|=（ ）
如图，二次函数y=ax2+bx+c图象的顶点D的横坐标为1，其图象与x轴的交点为A、B，3＜AB＜4，则|a-b+c|+|2a+b+c|=（ ）| A． | a-b | B． | 3a+2c | C． | a+2b | D． | -a-b |
10．
如图，用直尺和三角尺画图：已知点P和直线a，经过点P作直线b，使b∥a，其画法的依据是（ ）
如图，用直尺和三角尺画图：已知点P和直线a，经过点P作直线b，使b∥a，其画法的依据是（ ）| A． | 同位角相等，两直线平行 | |
| B． | 两直线平行，同位角相等 | |
| C． | 过直线外一点有且只有一条直线与已知直线平行 | |
| D． | 内错角相等，两直线平行 |
11．下列二次根式中，是最简二次根式的是（ ）
| A． | $\sqrt{0.5}$ | B． | $\sqrt{4a}$ | C． | $\sqrt{15}$ | D． | $\sqrt{\frac{1}{3}}$ |