题目内容
在开展垃圾不落地,学校更美丽活动中,学校决定购买一定数量的垃圾桶,现在某公司有A、B、C三种型号,信息如下:
(1)现在学校购买A、B两种型号垃圾桶共20个,已知购买费用不超过2300元,可供使用人数不少于1400人,有哪几种购买方案?
(2)若现在学校准备购买A、B、C三种型号垃圾桶若干个,投资恰好是1140元,可供使用人数达680人,则三种型号垃圾桶共购买多少个?
| 项目 | A型 | B型 | C型 |
| 销售价(元) | 120 | 100 | 70 |
| 可供使用人数(人) | 80 | 50 | 40 |
(2)若现在学校准备购买A、B、C三种型号垃圾桶若干个,投资恰好是1140元,可供使用人数达680人,则三种型号垃圾桶共购买多少个?
考点:一元一次不等式组的应用
专题:
分析:(1)设A种型号垃圾桶x个,则B种型号垃圾桶(20-x)个.数量关系有两个:购买费用不超过2300元,可供使用人数不少于1400人,据此列出不等式组;
(2)设A、B、C型号的垃圾桶分别是a、b、c个.依据数量关系“投资恰好是1140元,可供使用人数达680人”列出方程组.
(2)设A、B、C型号的垃圾桶分别是a、b、c个.依据数量关系“投资恰好是1140元,可供使用人数达680人”列出方程组.
解答:(1)解:设A种型号垃圾桶x个,则B种型号垃圾桶(20-x)个.则
解得
≤x≤15
∵x是正整数,
∴x=14或x=15,共有两种购买方案.
①A种型号垃圾桶14个,B种型号垃圾桶6个.
②A种型号垃圾桶15个,B种型号垃圾桶5个.
(2)设A、B、C型号的垃圾桶分别是a、b、c个.则
,
解得 2.5b-c=12.
∵a、b、c都是正整数,
∴a=4,b=4,c=2
则4+4+2=10
答:三种型号垃圾桶共购买10个.
|
解得
| 40 |
| 3 |
∵x是正整数,
∴x=14或x=15,共有两种购买方案.
①A种型号垃圾桶14个,B种型号垃圾桶6个.
②A种型号垃圾桶15个,B种型号垃圾桶5个.
(2)设A、B、C型号的垃圾桶分别是a、b、c个.则
|
解得 2.5b-c=12.
∵a、b、c都是正整数,
∴a=4,b=4,c=2
则4+4+2=10
答:三种型号垃圾桶共购买10个.
点评:本题考查了一元一次不等式组的应用,以及三元一次方程组的应用.注意,解题过程中的未知数都是正整数.

练习册系列答案
相关题目
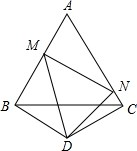 如图,△ABC是边长为a的等边三角形,△BCD中,BD=CD,∠BDC=120°,点M,N分别在AB,AC上,且∠MDN=60°.试问:△AMN的周长和面积是否随着点M,N的位置的改变而改变,请说明理由.
如图,△ABC是边长为a的等边三角形,△BCD中,BD=CD,∠BDC=120°,点M,N分别在AB,AC上,且∠MDN=60°.试问:△AMN的周长和面积是否随着点M,N的位置的改变而改变,请说明理由. 如图,抛物线y=ax2+bx+c,则a
如图,抛物线y=ax2+bx+c,则a 如图,抛物线y=ax2+bx+c与x轴的交点分别为(-1,0),(3,0),则
如图,抛物线y=ax2+bx+c与x轴的交点分别为(-1,0),(3,0),则