题目内容
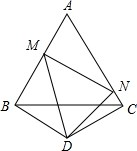 如图,△ABC是边长为a的等边三角形,△BCD中,BD=CD,∠BDC=120°,点M,N分别在AB,AC上,且∠MDN=60°.试问:△AMN的周长和面积是否随着点M,N的位置的改变而改变,请说明理由.
如图,△ABC是边长为a的等边三角形,△BCD中,BD=CD,∠BDC=120°,点M,N分别在AB,AC上,且∠MDN=60°.试问:△AMN的周长和面积是否随着点M,N的位置的改变而改变,请说明理由.考点:全等三角形的判定与性质,等边三角形的性质
专题:计算题
分析:△AMN的周长不变,面积发生变化,理由为:延长AB到E,使BE=CN,连接ED,由三角形ABC为等边三角形,利用等边三角形的性质得到∠ABC=∠ACB=60°,AB=AC=BC,再由三角形BCD为等腰三角形得到两底角相等,利用等式的性质得到夹角相等,利用SAS得到三角形EDM与三角形NDM全等,利用全等三角形的对应边相等得到ED=ND,再利用等式的性质得到夹角相等,利用SAS得到三角形EMD与三角形NMD全等,利用全等三角形对应边相等得到ME=MN,等量代换得到MN=MB+NC,表示出三角形AMN周长,等量代换求出周长为2a,而面积变化.
解答: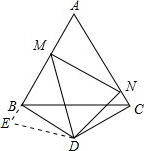 解:△AMN的周长不变,面积发生变化,
解:△AMN的周长不变,面积发生变化,
理由为:延长AB到E,使BE=CN,连接ED,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AB=AC,
∵△BCD中,BD=CD,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ABD=∠ACD=90°,
∴∠EBD=∠NCD=90°,
在△BED和△CND中,
,
∴△BED≌△CND(SAS),
∴ED=ND,∠BDE=∠CDN,
∵∠BDM+∠CDN=60°,
∴∠BDM+∠BDE=60°,即∠EDM=∠NDM,
在△EDM和△NDM中,
,
∴△EDM≌△NDM(SAS),
∴ME=MN,
∴MN=ME=MB+BE=MB+NC,
则△AMN周长为AM+AN+MN=AM+AN+MB+NC=AB+AC=2a,△AMN面积发生变化.
 解:△AMN的周长不变,面积发生变化,
解:△AMN的周长不变,面积发生变化,理由为:延长AB到E,使BE=CN,连接ED,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AB=AC,
∵△BCD中,BD=CD,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ABD=∠ACD=90°,
∴∠EBD=∠NCD=90°,
在△BED和△CND中,
|
∴△BED≌△CND(SAS),
∴ED=ND,∠BDE=∠CDN,
∵∠BDM+∠CDN=60°,
∴∠BDM+∠BDE=60°,即∠EDM=∠NDM,
在△EDM和△NDM中,
|
∴△EDM≌△NDM(SAS),
∴ME=MN,
∴MN=ME=MB+BE=MB+NC,
则△AMN周长为AM+AN+MN=AM+AN+MB+NC=AB+AC=2a,△AMN面积发生变化.
点评:此题考查了全等三角形的判定与性质,线段垂直平分线的性质,以及等腰直角三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 将图中的三张扑克牌背面朝上放在桌面上,从中随机摸出两张,并用这两张扑克牌上的数字组成一个两位数.请用画树状图(或列表)的方法,求组成的两位数是偶数的概率.
将图中的三张扑克牌背面朝上放在桌面上,从中随机摸出两张,并用这两张扑克牌上的数字组成一个两位数.请用画树状图(或列表)的方法,求组成的两位数是偶数的概率.