题目内容
11.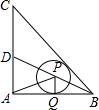 如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=1,BD平方∠ABC,点P在BD上,⊙P切AB于点Q,则AP+PQ的最小值等于$\frac{\sqrt{2}}{2}$.
如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=1,BD平方∠ABC,点P在BD上,⊙P切AB于点Q,则AP+PQ的最小值等于$\frac{\sqrt{2}}{2}$.
分析 过点A作AM⊥BC于点M,交BD于点P′,过点P′作P′Q′⊥AB于点Q′,因为BD平分∠ABC,所以P′Q′=P′M,这时AP′+P′Q′有最小值,即AM的长度,当P和P′重合时,AP+PQ的最小值就是AM的长,运用勾股定理求出BC,再根据直角三角形斜边中线的性质得出AM的值,即AP+PQ的最小值.
解答 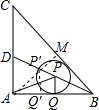 解:如图,过点A作AM⊥BC于点M,交BD于点P′,过点P′作P′Q′⊥AB于点Q′,
解:如图,过点A作AM⊥BC于点M,交BD于点P′,过点P′作P′Q′⊥AB于点Q′,
∵BD平分∠ABC.
∴P′Q′=P′M,这时AP′+P′Q′有最小值,即AM的长度,
∴当P和P′重合时,AP+PQ的最小值就是AM的长,
∵AB=AC=1,∠BAC=90°,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{2}$.
∵△ABC是等腰直角三角形,
∴AM是直角三角形斜边的中线,
∴AM=$\frac{1}{2}$BC=$\frac{\sqrt{2}}{2}$
即PC+PQ的最小值为$\frac{\sqrt{2}}{2}$,
故答案为$\frac{\sqrt{2}}{2}$.
点评 本题主要考查了轴对称问题,解题的关键是找出满足AP+PQ有最小值时点P和Q的位置.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
2. 如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
 如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | $\sqrt{8}$ | B. | 3 | C. | 4 | D. | 2 |
6.已知△ABC中,AB=3,BC=4,AC的长是方程x2-12x+35=0的根,则△ABC的周长等于( )
| A. | 12 | B. | 14 | C. | 12或14 | D. | 以上都不是 |
20.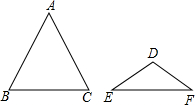 如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )
如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )
 如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )
如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )| A. | 9:4 | B. | 3:2 | C. | $\sqrt{3}:\sqrt{2}$ | D. | $3\sqrt{3}:2\sqrt{2}$ |
 如图,在菱形ABCD中,cosA=$\frac{3}{5}$,BE=2,则tan∠BDE=2.
如图,在菱形ABCD中,cosA=$\frac{3}{5}$,BE=2,则tan∠BDE=2.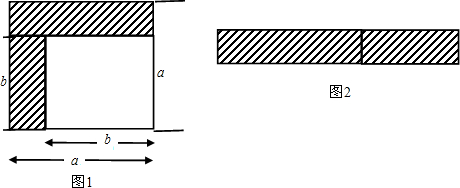
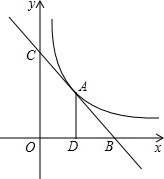 已知直线y=k1x+b与双曲线$y=\frac{k_2}{x}$相交于点A(2,4),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,求直线和双曲线的解析式.
已知直线y=k1x+b与双曲线$y=\frac{k_2}{x}$相交于点A(2,4),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,求直线和双曲线的解析式. 从化市某中学初三(1)班数学兴趣小组为了解全校800名初三学生的“初中毕业选择升学和就业”情况,特对本班50名同学们进行调查,根据全班同学提出的3个主要观点:A高中,B中技,C就业,进行了调查(要求每位同学只选自己最认可的一项观点);并制成了扇形统计图(如图).请回答以下问题:
从化市某中学初三(1)班数学兴趣小组为了解全校800名初三学生的“初中毕业选择升学和就业”情况,特对本班50名同学们进行调查,根据全班同学提出的3个主要观点:A高中,B中技,C就业,进行了调查(要求每位同学只选自己最认可的一项观点);并制成了扇形统计图(如图).请回答以下问题: