题目内容
3.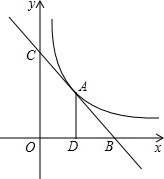 已知直线y=k1x+b与双曲线$y=\frac{k_2}{x}$相交于点A(2,4),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,求直线和双曲线的解析式.
已知直线y=k1x+b与双曲线$y=\frac{k_2}{x}$相交于点A(2,4),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,求直线和双曲线的解析式.
分析 把A(2,4)代入$y=\frac{k_2}{x}$求出k2=8,得出双曲线的解析式,根据A(2,4),AD⊥OB,AD平分OB求出OB=4,求出B的坐标,把A、B的坐标代入y=k1x+b得出方程组,求出方程组的解,即可得出直线的解析式.
解答 解:∵双曲线$y=\frac{k_2}{x}$经过点A(2,4)
∴k2=8,
∴双曲线的解析式为y=$\frac{8}{x}$,
∵A(2,4),AD⊥OB,AD平分OB,
∴OB=4,B(4,0),
∵直线y=k1x+b经过点A(2,4),B(4,0)
∴$\left\{\begin{array}{l}{2{k}_{1}+b=4}\\{4{k}_{1}+b=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{{k}_{1}=-2}\\{b=8}\end{array}\right.$
∴直线的解析式为y=-2x+8,
点评 本题考查了一次函数与反比例函数的交点问题,用待定系数法求函数的解析式的应用,主要考查学生的计算能力.

练习册系列答案
相关题目
14.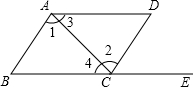 如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
 如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠B=∠DCE | C. | ∠1=∠2 | D. | ∠D+∠DAB=180° |
15.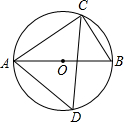 如图,AB是⊙O的直径,若∠ADC=55°,则∠BAC的大小是( )
如图,AB是⊙O的直径,若∠ADC=55°,则∠BAC的大小是( )
 如图,AB是⊙O的直径,若∠ADC=55°,则∠BAC的大小是( )
如图,AB是⊙O的直径,若∠ADC=55°,则∠BAC的大小是( )| A. | 35° | B. | 55° | C. | 70° | D. | 110° |
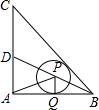 如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=1,BD平方∠ABC,点P在BD上,⊙P切AB于点Q,则AP+PQ的最小值等于$\frac{\sqrt{2}}{2}$.
如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=1,BD平方∠ABC,点P在BD上,⊙P切AB于点Q,则AP+PQ的最小值等于$\frac{\sqrt{2}}{2}$.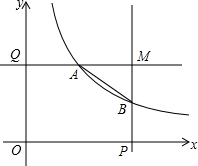 如图,在平面直角坐标系中,P,Q分别是x轴,y轴的正半轴上两动点,OP=2,OQ=k,分别过P,Q作坐标轴的垂线,交反比例函数y=$\frac{k}{x}$于点A,B两垂线交于点M,点E为线段OP上一动点.
如图,在平面直角坐标系中,P,Q分别是x轴,y轴的正半轴上两动点,OP=2,OQ=k,分别过P,Q作坐标轴的垂线,交反比例函数y=$\frac{k}{x}$于点A,B两垂线交于点M,点E为线段OP上一动点.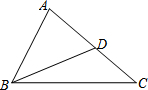 如图,△ABC中,D是边AC上一点,连接BD.要使△ABD∽△ACB,需要补充的一个条件为∠ABD=∠C或∠ADB=∠ABC或AB2=AD•AC.
如图,△ABC中,D是边AC上一点,连接BD.要使△ABD∽△ACB,需要补充的一个条件为∠ABD=∠C或∠ADB=∠ABC或AB2=AD•AC.