题目内容
6.已知△ABC中,AB=3,BC=4,AC的长是方程x2-12x+35=0的根,则△ABC的周长等于( )| A. | 12 | B. | 14 | C. | 12或14 | D. | 以上都不是 |
分析 先求出方程的解,再根据三角形的三边关系定理判断是否能组成三角形,最后求出即可.
解答 解:x2-12x+35=0,
(x-5)(x-7)=0,
x-5=0,x-7=0,
x1=5,x2=7,
①当三角形的三边为3,4,5时,符合三角形三边关系定理,即△ABC的周长为3+4+5=12;
②当三角形的三边为3,4,7时,不符合三角形三边关系定理,此时三角形不存在;
故选A.
点评 本题考查了三角形的三边关系定理,解一元二次方程的应用,解此题的关键是能求出符合条件的所有情况,难度适中.

练习册系列答案
相关题目
16.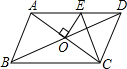 如图,?ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为( )
如图,?ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为( )
 如图,?ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为( )
如图,?ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
17.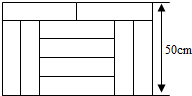 如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
 如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )| A. | 400cm2 | B. | 500cm2 | C. | 600cm2 | D. | 4000cm2 |
14.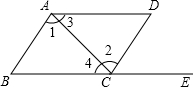 如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
 如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠B=∠DCE | C. | ∠1=∠2 | D. | ∠D+∠DAB=180° |
1.在平面直角坐标系中将点P(2,-3)向上平移4个单位后得到点Q,则点Q的坐标是( )
| A. | (2,1) | B. | (2,-7) | C. | (6,-3) | D. | (-2,-3) |
15.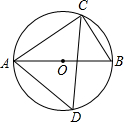 如图,AB是⊙O的直径,若∠ADC=55°,则∠BAC的大小是( )
如图,AB是⊙O的直径,若∠ADC=55°,则∠BAC的大小是( )
 如图,AB是⊙O的直径,若∠ADC=55°,则∠BAC的大小是( )
如图,AB是⊙O的直径,若∠ADC=55°,则∠BAC的大小是( )| A. | 35° | B. | 55° | C. | 70° | D. | 110° |
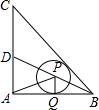 如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=1,BD平方∠ABC,点P在BD上,⊙P切AB于点Q,则AP+PQ的最小值等于$\frac{\sqrt{2}}{2}$.
如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=1,BD平方∠ABC,点P在BD上,⊙P切AB于点Q,则AP+PQ的最小值等于$\frac{\sqrt{2}}{2}$.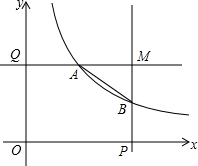 如图,在平面直角坐标系中,P,Q分别是x轴,y轴的正半轴上两动点,OP=2,OQ=k,分别过P,Q作坐标轴的垂线,交反比例函数y=$\frac{k}{x}$于点A,B两垂线交于点M,点E为线段OP上一动点.
如图,在平面直角坐标系中,P,Q分别是x轴,y轴的正半轴上两动点,OP=2,OQ=k,分别过P,Q作坐标轴的垂线,交反比例函数y=$\frac{k}{x}$于点A,B两垂线交于点M,点E为线段OP上一动点.