题目内容
2. 如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | $\sqrt{8}$ | B. | 3 | C. | 4 | D. | 2 |
分析 由于点B与D关于AC对称,所以连接BE,与AC的交点即为P点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为4,可求出AB的长,从而得出结果.
解答 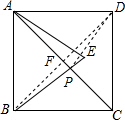 解:连接BD,与AC交于点F.
解:连接BD,与AC交于点F.
∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的面积为4,
∴AB=2.
又∵△ABE是等边三角形,
∴BE=AB=2.
∴所求最小值为2.
故选:D.
点评 此题主要考查了轴对称--最短路线问题,难点主要是确定点P的位置.注意充分运用正方形的性质:正方形的对角线互相垂直平分.再根据对称性确定点P的位置即可.要灵活运用对称性解决此类问题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
12.函数y=$\frac{k}{x}$的图象经过点(2,1),则k的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
10.“H7N9”是一种新型禽流感,其病毒颗粒呈多形性,其汇总球形病毒的最大直径为0.00000012米,这一直径用科学记数法表示为( )
| A. | 1.2×10-9米 | B. | 1.2×10-8米 | C. | 1.2×10-7米 | D. | 12×10-9米 |
17.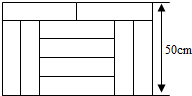 如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
 如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )| A. | 400cm2 | B. | 500cm2 | C. | 600cm2 | D. | 4000cm2 |
7.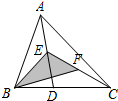 如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
 如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )| A. | 1cm2 | B. | 2cm2 | C. | 8cm2 | D. | 16cm2 |
14.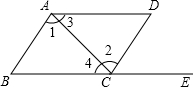 如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
 如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠B=∠DCE | C. | ∠1=∠2 | D. | ∠D+∠DAB=180° |
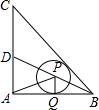 如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=1,BD平方∠ABC,点P在BD上,⊙P切AB于点Q,则AP+PQ的最小值等于$\frac{\sqrt{2}}{2}$.
如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=1,BD平方∠ABC,点P在BD上,⊙P切AB于点Q,则AP+PQ的最小值等于$\frac{\sqrt{2}}{2}$.