题目内容
12.P是∠AOB内一点,OP平分∠AOB,PA⊥OA,PB⊥OB,C是射线OA上不与点A重合的一点,D是射线OB上不与点B重合的一点,且AC=BD,下列结论:①PA=PB; ②PO平分∠APB;③OC=OD; ④△PAC≌△PBD;其中一定成立的是①②④(只需填序号)分析 画出图形,可以证明△OPA≌△OPB,△PAC≌△PBD由此一一判断即可.
解答 解:如图,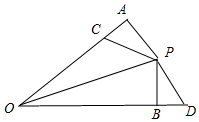
∵OP平分∠AOB,
∴∠OPA=∠POB,
∵PA⊥OA,PB⊥OB,
∴∠OBP=90°,
在△OPA和△OPB中,
$\left\{\begin{array}{l}{∠OAP=∠OBP}\\{∠POA=∠POB}\\{OP=OP}\end{array}\right.$,
∴△OPA≌△OPB,
∴PA=PB,∠OPA=∠OPB,
∴OP平分∠APB,故①②正确,
在△PAC和△PBD中,
$\left\{\begin{array}{l}{PA=PB}\\{∠A=∠OBD}\\{AC=BD}\end{array}\right.$,
∴△PAC≌△PBD,故④正确,
∵OC≠OD,故③错误,
故答案为①②④.
点评 本题考查全等三角形的判定和性质、角平分线的性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,学会用分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
7. 数a、b、c在数轴上对应的位置如图,化简|a+b|-|c-b|的结果( )
数a、b、c在数轴上对应的位置如图,化简|a+b|-|c-b|的结果( )
 数a、b、c在数轴上对应的位置如图,化简|a+b|-|c-b|的结果( )
数a、b、c在数轴上对应的位置如图,化简|a+b|-|c-b|的结果( )| A. | a+c | B. | c-a | C. | -c-a | D. | a+2b-c |
4.下列各数-2,3,-(-0.75),-5.4,|-9|,-3,0,4中,属于整数的有( )个,属于正数的有( )个.
| A. | 6,4 | B. | 5,5 | C. | 4,3 | D. | 3,6 |
1.下列长度的各组线段中,能组成三角形的是( )
| A. | 6,6,11 | B. | 8,8,16 | C. | 4,5,10 | D. | 6,7,14 |