题目内容
16.如图图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,
(1)按此规律,图案⑦需50根火柴棒;第n个图案需7n+1根火柴棒.
(2)用2017根火柴棒能按规律拼搭而成一个图案?若能,说明是第几个图案:若不可能,请说明理由.
分析 (1)根据图案①、②、③中火柴棒的数量可知,第1个图形中火柴棒有8根,每多一个多边形就多7根火柴棒,由此可知第n个图案需火柴棒8+7(n-1)=7n+1根,令n=7可得答案.
(2)令8+7(n-1)=7n+1=2017求得n值即可.
解答 解:(1)∵图案①需火柴棒:8根;
图案②需火柴棒:8+7=15根;
图案③需火柴棒:8+7+7=22根;
…
∴图案n需火柴棒:8+7(n-1)=7n+1根;
当n=7时,7n+1=7×7+1=50,
∴图案⑦需50根火柴棒;
故答案为:50,7n+1.
(2)令7n+1=2017,
解得n=288,
故2017是第288个图案.
点评 此题主要考查了图形的变化类,解决此类题目的关键在于图形在变化过程中准确抓住不变的部分和变化的部分,变化部分是以何种规律变化.

练习册系列答案
相关题目
7.某公司产销一种产品,为保证质量,每个周期产销商品件数控制在100以内,产销成本C是商品件数x的二次函数,调查数据如表:
商品的销售价格(单位:元)为P=35-$\frac{1}{10}$x(每个周期的产销利润=P•x-C)
(1)直接写出产销成本C与商品件数x的函数关系式(不要求写出自变量的取值范围)
(2)该公司每个周期产销多少件商品时,利润达到220元?
(3)求该公司每个周期的产销利润的最大值.
| 产销商品件数(x/件) | 10 | 20 | 30 |
| 产销成本(C/元) | 120 | 180 | 260 |
(1)直接写出产销成本C与商品件数x的函数关系式(不要求写出自变量的取值范围)
(2)该公司每个周期产销多少件商品时,利润达到220元?
(3)求该公司每个周期的产销利润的最大值.
1.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如表:
已知日销售量y是销售价x的一次函数.
(1)求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;
(2)当每件产品的销售价定为35元时,此时每日的销售利润是多少元?
| x/元 | … | 15 | 20 | 25 | … |
| y/件 | … | 25 | 20 | 15 | … |
(1)求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;
(2)当每件产品的销售价定为35元时,此时每日的销售利润是多少元?
3.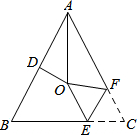 如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )
如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )
 如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )
如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )| A. | 106° | B. | 108° | C. | 110° | D. | 112° |

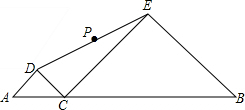 如图,线段AB长为6,点C是线段AB上一动点(不与A,B重合)分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1处沿AB向右运动至距离B点1处时,点P运动的路径长是2.
如图,线段AB长为6,点C是线段AB上一动点(不与A,B重合)分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1处沿AB向右运动至距离B点1处时,点P运动的路径长是2.