题目内容
4．计算$\frac{tan45°}{sin30°}$-$\frac{cos45°}{sin60°•tan60°}$．分析 根据特殊角三角函数值，可得答案．
解答 解：原式=$\frac{1}{\frac{1}{2}}$-$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}×\sqrt{3}}$=2-$\frac{\sqrt{2}}{3}$．
点评 本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键．
练习册系列答案
相关题目
如图，将△ABE向右平移2cm得到△DCF，如果△ABE的周长是16cm，那么四边形ABFD的周长是20cm．
15．
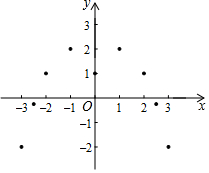某“数学兴趣小组”根据学习函数的经验，对函数y=-x2+2|x|+1的图象和性质进行了探究，探究过程如下，请补充完整：
（1）自变量x的取值范围是全体实数，x与y的几组对应数值如表：
其中m=1；
（2）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（3）根据函数图象，写出：
①该函数的一条性质函数图象关于y轴对称；
②直线y=kx+b经过点（-1，2），若关于x的方程-x2+2|x|+1=kx+b有4个互不相等的实数根，则b的取值范围是1＜b＜2．
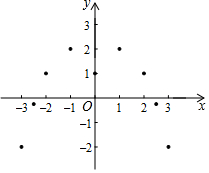某“数学兴趣小组”根据学习函数的经验，对函数y=-x2+2|x|+1的图象和性质进行了探究，探究过程如下，请补充完整：（1）自变量x的取值范围是全体实数，x与y的几组对应数值如表：
| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | -2 | -$\frac{1}{4}$ | m | 2 | 1 | 2 | 1 | -$\frac{1}{4}$ | -2 | … |
（2）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（3）根据函数图象，写出：
①该函数的一条性质函数图象关于y轴对称；
②直线y=kx+b经过点（-1，2），若关于x的方程-x2+2|x|+1=kx+b有4个互不相等的实数根，则b的取值范围是1＜b＜2．
12．北京故宫是中国明清两代的皇家宫殿，旧称为紫禁城，是中国古代宫廷建筑之精华，深受国内外游客的喜爱．据报道，北京故宫在2015年全年参观的总人数约为15 060 000人．将15 060 000用科学记数法表示为（ ）
| A． | 1.506×108 | B． | 1.506×107 | C． | 15.06×106 | D． | 15.06×107 |
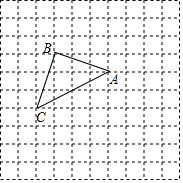如图，所有小正方形的边长都为1，A、B、C都在格点上．