题目内容
已知?ABCD中，AB=5，AC=8，∠A=120°，过点A任意引直线l，设顶点B、C、D到l的距离之和为d．求d的最大值．
考点：平行四边形的性质
专题：
分析：作出图形，根据垂线段最短判断出CA⊥l时，点D到直线l的距离最大，再根据梯形的中位线等于两底和的一半解答．
解答：
解：由垂线段最短可知，CA⊥直线l时，点C到直线l的距离最大，
此时，由梯形中位线定理，B、D到直线l的距离之和的最大值=2AO=AC=8，
所以d的最大值=2AC=2×8=16．
解：由垂线段最短可知，CA⊥直线l时，点C到直线l的距离最大，此时，由梯形中位线定理，B、D到直线l的距离之和的最大值=2AO=AC=8，
所以d的最大值=2AC=2×8=16．
点评：本题考查了梯形中位线，从点B、D到直线l的距离考虑利用梯形中位线定理求解是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
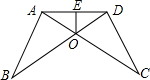
如图，∠BDA=∠CEA，AE=AD．求证：AB=AC．
如图，AB=CD，∠B=∠C，AC和BD相交于点O，E是AD的中点，连接OE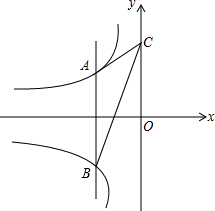
如图，动点A在双曲线y=-
（1）已知：如图，∠BAC=∠DCA，∠BCA=∠DAC，求证：△ABC≌△CDA．