题目内容
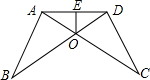 如图,AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE
如图,AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE(1)试说明△AOB与△DOC全等;
(2)OE与AD具有怎样的位置关系?请说明理由.
考点:全等三角形的判定与性质
专题:
分析:(1)由已知加上对顶角相等,利用AAS即可得证;
(2)OE与AD垂直,理由为:根据(1)的结论,利用全等三角形对应边相等得到OA=OD,再由OE为AD上的中线,利用三线合一即可得证.
(2)OE与AD垂直,理由为:根据(1)的结论,利用全等三角形对应边相等得到OA=OD,再由OE为AD上的中线,利用三线合一即可得证.
解答:(1)证明:在△AOB和△DOC中,
,
∴△AOB≌△DOC(AAS);
(2)OE⊥AD,理由为:
证明:∵△AOB≌△DOC,
∴OA=OD,
∵E为AD的中点,
∴OE⊥AD.
|
∴△AOB≌△DOC(AAS);
(2)OE⊥AD,理由为:
证明:∵△AOB≌△DOC,
∴OA=OD,
∵E为AD的中点,
∴OE⊥AD.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,OA=OB,OC=OD,∠AOC=∠BOD,求证:AB∥CD.
如图,OA=OB,OC=OD,∠AOC=∠BOD,求证:AB∥CD.
 如图,AE=AF,点B、D分别在AE、AF上,四边形ABCD是菱形,连接EC、FC
如图,AE=AF,点B、D分别在AE、AF上,四边形ABCD是菱形,连接EC、FC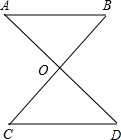 (1)计算:(π-3)0+
(1)计算:(π-3)0+