题目内容
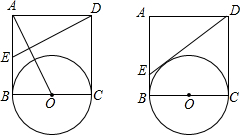
将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.如果AD=
,则菱形AECF的周长为 .

| 3 |

考点:翻折变换(折叠问题)
专题:
分析:根据翻折的性质可得∠DAF=∠OAF,根据菱形的对角线平分一组对角线可得∠OAF=∠OAE,然后求出∠DAF=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得DF=
AF,然后利用勾股定理列出方程求出AF,再根据菱形的四条边都相等求解即可.
| 1 |
| 2 |
解答:解:由折叠的性质得,∠DAF=∠OAF,
∵四边形AECF是菱形,
∴∠OAF=∠OAE,
∴∠DAF=
×90°=30°,
∴DF=
AF,
在Rt△ADF中,AD2+DF2=AF2,
所以,(
)2+(
AF)2=AF2,
解得AF=2,
所以菱形AECF的周长=4AF=4×2=8.
故答案为:8.
∵四边形AECF是菱形,
∴∠OAF=∠OAE,
∴∠DAF=
| 1 |
| 3 |
∴DF=
| 1 |
| 2 |
在Rt△ADF中,AD2+DF2=AF2,
所以,(
| 3 |
| 1 |
| 2 |
解得AF=2,
所以菱形AECF的周长=4AF=4×2=8.
故答案为:8.
点评:本题考查了翻折变换的性质,菱形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,勾股定理,熟记各性质并求出∠DAF=30°是解题的关键.

练习册系列答案
相关题目