题目内容
15.在Rt△ABC中,∠C=90°,AC=BC,若以点C为圆心,以2cm长为半径的圆与斜边AB相切,那么BC的长等于( )| A. | 2cm | B. | 2$\sqrt{2}$cm | C. | 2$\sqrt{3}$cm | D. | 4cm |
分析 根据题意画出图形,再根据勾股定理求出BC的长即可.
解答  解:如图所示,
解:如图所示,
∵在Rt△ABC中,∠C=90°,AC=BC,CD⊥AB,
∴△ABC是等腰直角三角形.
∵以点C为圆心,以2cm长为半径的圆与斜边AB相切,
∴CD=2cm,
∵∠B=45°,
∴CD=BD=2,
∴BC=$\sqrt{{CD}^{2}+{BD}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$(cm).
故选B.
点评 本题考查的是直线与圆的位置关系,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
10.已知⊙O的半径为6cm,圆心O到直线l的距离为5cm,则直线l与⊙O的交点个数为( )
| A. | 0 | B. | l | C. | 2 | D. | 无法确定 |
4.若要使分式$\frac{3x^{2}-6x+3}{(x-1)^{3}}$的值为整数,则整数x可取的个数为( )
| A. | 5个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.下列方程中,一元二次方程的是( )
| A. | 2x-x2=0 | B. | 3(x-2)+x=1 | C. | x2-2xy-3y2=0 | D. | $\frac{1}{{x}^{2}}$-x+3=0 |
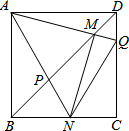 如图,边长为1的正方形ABCD,Q是CD上一动点(不与点C、D重合),连接AQ交BD于点M,过M作MN⊥AQ交BC于N点,连接AN交BD于点P,在点Q运动过程中有下列结论:①AM=MN;②BM•DP=1;③存在点Q,使得BN+DQ=1;④$\sqrt{2}$BM-BN=1.其中一定成立的是①②④.
如图,边长为1的正方形ABCD,Q是CD上一动点(不与点C、D重合),连接AQ交BD于点M,过M作MN⊥AQ交BC于N点,连接AN交BD于点P,在点Q运动过程中有下列结论:①AM=MN;②BM•DP=1;③存在点Q,使得BN+DQ=1;④$\sqrt{2}$BM-BN=1.其中一定成立的是①②④.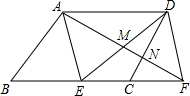 在?ABCD中,点E在BC边上,点F在BC边的延长线上,且BE=CF.
在?ABCD中,点E在BC边上,点F在BC边的延长线上,且BE=CF.