题目内容
4.若要使分式$\frac{3x^{2}-6x+3}{(x-1)^{3}}$的值为整数,则整数x可取的个数为( )| A. | 5个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 首先化简分式可得$\frac{3}{x-1}$,要使它的值为整数,则(x-1)应是3的约数,即x-1=±1或±3,进而解出x的值.
解答 解:∵$\frac{3{x}^{2}-6x+3}{(x-1)^{3}}=\frac{3(x-1)^{2}}{(x-1)^{3}}=\frac{3}{x-1}$,
∴根据题意,得x-1=±1或±3,
解得x=0或x=2或x=-2或x=4,
故选D.
点评 此题考查分式的值,此类题首先要正确化简分式,然后要保证分式的值为整数,则根据分母应是分子的约数,进行分析.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
14.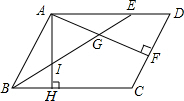 在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )
在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )
 在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )
在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 6 | D. | 3$\sqrt{3}$ |
15.在Rt△ABC中,∠C=90°,AC=BC,若以点C为圆心,以2cm长为半径的圆与斜边AB相切,那么BC的长等于( )
| A. | 2cm | B. | 2$\sqrt{2}$cm | C. | 2$\sqrt{3}$cm | D. | 4cm |
19.已知等腰三角形的两条边长分别为2和3,则它的周长为( )
| A. | 7 | B. | 8 | C. | 5 | D. | 7或8 |

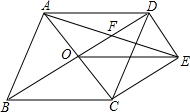 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=$\frac{1}{2}$AC,连接 CE、OE,连接AE交OD于点F.
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=$\frac{1}{2}$AC,连接 CE、OE,连接AE交OD于点F.