题目内容
3.(1)先化简,再求值:(2x+3y)2-(2x+y)(2x-y),其中x=$\frac{1}{3}$,y=$-\frac{1}{2}$.(2)因式分解:(p2-16)(p2+1)+15p2.
分析 (1)先算乘法,再合并同类项,最后代入求出即可;
(2)先展开,合并后根据平方差公式分解即可.
解答 解:(1)(2x+3y)2-(2x+y)(2x-y)
=4x2+12xy+9y2-4x2+y2
=12xy+10y2,
当x=$\frac{1}{3}$,y=$-\frac{1}{2}$时,原式=12×$\frac{1}{3}$×(-$\frac{1}{2}$)+10×(-$\frac{1}{2}$)2=$\frac{1}{2}$;
(2)(p2-16)(p2+1)+15p2
=p4-15p2-16+15p2
=p4-16
=(p2+4)(p2-4)
=(p2+4)(p+2)(p-2).
点评 本题考查了整式的混合运算和求值,分解因式的应用,能正确运用整式的运算法则进行化简和能选择适当的方法分解因式是解此题的关键,难度适中.

练习册系列答案
相关题目
9.下列函数中,当x>0时,y随x的增大而减小的是( )
| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{4}{x}$ | C. | y=3x+2 | D. | y=x2-3 |
14.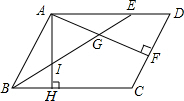 在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )
在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )
 在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )
在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 6 | D. | 3$\sqrt{3}$ |
18.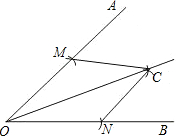 如图,已知∠AOB,按照以下步骤画图:
如图,已知∠AOB,按照以下步骤画图:
(1)以O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M、N为圆心,大于$\frac{1}{2}$MN的长半径画弧,两弧在∠AOB内部相交于点C.
(3)作射线OC.
则判断△OMC≌△ONC的依据是( )
 如图,已知∠AOB,按照以下步骤画图:
如图,已知∠AOB,按照以下步骤画图:(1)以O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M、N为圆心,大于$\frac{1}{2}$MN的长半径画弧,两弧在∠AOB内部相交于点C.
(3)作射线OC.
则判断△OMC≌△ONC的依据是( )
| A. | 边边边 | B. | 边角边 | C. | 角边角 | D. | 角角边 |
15.在Rt△ABC中,∠C=90°,AC=BC,若以点C为圆心,以2cm长为半径的圆与斜边AB相切,那么BC的长等于( )
| A. | 2cm | B. | 2$\sqrt{2}$cm | C. | 2$\sqrt{3}$cm | D. | 4cm |