题目内容
 如图,PA⊥OA于点A,PB⊥OB于点B,你认为再添加下列哪个条件也不能推出OP垂直平分AB( )
如图,PA⊥OA于点A,PB⊥OB于点B,你认为再添加下列哪个条件也不能推出OP垂直平分AB( )| A、OP⊥AB |
| B、OP平分∠AOB |
| C、PA=PB |
| D、∠OPA=∠OPB |
考点:角平分线的性质,全等三角形的判定与性质,线段垂直平分线的性质
专题:
分析:根据角平分线上的点到角的两边距离相等考虑OP是∠AOB或∠APB的平分线即可.
解答:解:若OP平分∠AOB,
∵PA⊥OA,PB⊥OB,
∴PA=PB,
在Rt△AOP和Rt△BOP中,
,
∴Rt△AOP≌Rt△BOP(HL),
∴OA=OB,
∴OP垂直平分AB,
PA=PB时,∵PA⊥OA,PB⊥OB,
∴OP平分∠AOB,
∠OPA=∠OPB时,同理可证OP垂直平分AB,
所以,不能推出OP垂直平分AB的是OP⊥AB.
故选A.
∵PA⊥OA,PB⊥OB,
∴PA=PB,
在Rt△AOP和Rt△BOP中,
|
∴Rt△AOP≌Rt△BOP(HL),
∴OA=OB,
∴OP垂直平分AB,
PA=PB时,∵PA⊥OA,PB⊥OB,
∴OP平分∠AOB,
∠OPA=∠OPB时,同理可证OP垂直平分AB,
所以,不能推出OP垂直平分AB的是OP⊥AB.
故选A.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记各性质以及三角形全等的判定方法是解题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目


 如图,在△ABC中,D为AB边上一点,∠B=∠ACD,若AD=4,BD=3,求AC的长.
如图,在△ABC中,D为AB边上一点,∠B=∠ACD,若AD=4,BD=3,求AC的长.

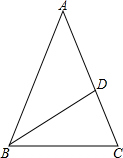 如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于D.
如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于D.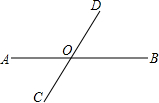 如图,直线AB,CD相交于点O,∠AOD比∠BOD大60°,求∠AOD与∠BOD的大小.
如图,直线AB,CD相交于点O,∠AOD比∠BOD大60°,求∠AOD与∠BOD的大小.