题目内容
如图，在△ABC中，D为AB边上一点，∠B=∠ACD，若AD=4，BD=3，求AC的长．考点：相似三角形的判定与性质
专题：
分析：由条件可证得△ABC∽△ACD，可得到
=
，从而可求得AC的长．
| AC |
| AD |
| AB |
| AC |
解答：证明：∵∠B=∠ACD，
又∴∠A=∠A，
∴△ABC∽△ACD，
∵
=
，
∴AC2=AD•AB．
∵AD=4，BD=3，
∴AB=7，
∴AC=2
．
又∴∠A=∠A，
∴△ABC∽△ACD，
∵
| AC |
| AD |
| AB |
| AC |
∴AC2=AD•AB．
∵AD=4，BD=3，
∴AB=7，
∴AC=2
| 7 |
点评：本题主要考查相似三角形的判定和性质，掌握利用两组角对应相等可判定两个三角形相似是解题的关键，把线段的乘积化为比例来证明是解这类问题的一般思路．
练习册系列答案
相关题目
如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC上，BD=1，DC=2，点P是AB上的动点，则PC+PD的最小值为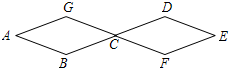
如图所示，两个全等菱形的边长为1厘米，一只蚂蚁由A点开始按ABCDEF的顺序按菱形的边循环运动，行走2015厘米后停下，则这只蚂蚁停在（ ）
如图，PA⊥OA于点A，PB⊥OB于点B，你认为再添加下列哪个条件也不能推出OP垂直平分AB（ ）| A、OP⊥AB |
| B、OP平分∠AOB |
| C、PA=PB |
| D、∠OPA=∠OPB |
老师布置了一道考题：如图所示，点M、N分别在正△ABC的边BC、CA上，且BM=CN，AM交BN于点Q．
把两个完全相同的矩形按如图所示的方式叠合起来；若矩形的长与宽分别为8cm与6cm，则重叠部分的面积为