题目内容
有一串数：-2003，-1999，-1995，-1991，┉，按一定的规律排列，那么这串数中前（ ）个数的和最小．
| A、500 | B、501 |
| C、502 | D、503 |
考点：规律型：数字的变化类
专题：规律型
分析：此题可联系数轴进行解答，从数轴的左侧-2003这个点开始，向右是等差数列，到达-3这个点时都在原点的左侧，再向右就到了原点的右侧的点1、3、5…，此时求和会越来越大，因此在原点左侧所有数的和最小，得出答案．
解答：解：这串数：-2003，-1999，-1995，-1991，┉，是等差数列，
最大的负数是-3，[（-3）-（-2003）]÷4+1=501
故选：B．
最大的负数是-3，[（-3）-（-2003）]÷4+1=501
故选：B．
点评：此题的解答搞清这串数是连续的奇数，再结合数轴进行解答即可解决问题．
练习册系列答案
相关题目
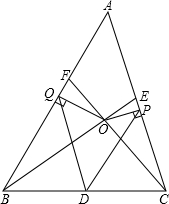如图，在△ABC中，D为BC的中点，点E、F分别在边AC、AB上，并且∠ABE=∠ACF，BE、CF交于点O．过点O作OP⊥AC，OQ⊥AB，P、Q为垂足．求证：DP=DQ．已知：-1＜b＜a＜0，那么a+b，a-b，a+1，a-1的大小关系是（ ）
| A、a+b＜a-b＜a-1＜a+1 |
| B、a+1＞a+b＞a-b＞a-1 |
| C、a-1＜a+b＜a-b＜a+1 |
| D、a+b＞a-b＞a+1＞a-1 |