题目内容
方程|x-|2x+1||=3的解的个数是( )
| A、0个 | B、1个 | C、2个 | D、无穷多 |
考点:含绝对值符号的一元一次方程
专题:计算题
分析:先根据绝对值的性质去掉外面的绝对值,然后运用零点讨论法,①x≥-
,②x<-
,分别解出方程的解即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵|x-|2x+1||=3,
∴x-|2x+1|=3或x-|2x+1|=-3.
则|2x+1|=x-3或|2x+1|=x+3.
①当|2x+1|=x-3时:
当x≥-
时,原方程变形为2x+1=x-3,
解得x=-4(舍);
当x<-
时,原方程变形为2x+1=3-x,
x=
(舍);
②当|2x+1|=x+3时:
当x≥-
时,原方程变形为2x+1=x+3,
解得x=2,
当x<-
时,原方程变形为2x+1=-x-3,
解得x=-
.
经检验:x=2,x=-
是原方程的解,共两个.
故选C.
∴x-|2x+1|=3或x-|2x+1|=-3.
则|2x+1|=x-3或|2x+1|=x+3.
①当|2x+1|=x-3时:
当x≥-
| 1 |
| 2 |
解得x=-4(舍);
当x<-
| 1 |
| 2 |
x=
| 2 |
| 3 |
②当|2x+1|=x+3时:
当x≥-
| 1 |
| 2 |
解得x=2,
当x<-
| 1 |
| 2 |
解得x=-
| 4 |
| 3 |
经检验:x=2,x=-
| 4 |
| 3 |
故选C.
点评:本题考查含绝对值的一元一次方程,难度较大,关键是利用绝对值的性质先去掉一个绝对值,注意在得出解后要检验.

练习册系列答案
相关题目
已知:m2+m-1=0,那么代数式m3+2m2-1997的值是( )
| A、1997 | B、-1997 |
| C、1996 | D、-1996 |
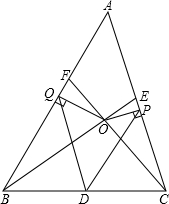 如图,在△ABC中,D为BC的中点,点E、F分别在边AC、AB上,并且∠ABE=∠ACF,BE、CF交于点O.过点O作OP⊥AC,OQ⊥AB,P、Q为垂足.求证:DP=DQ.
如图,在△ABC中,D为BC的中点,点E、F分别在边AC、AB上,并且∠ABE=∠ACF,BE、CF交于点O.过点O作OP⊥AC,OQ⊥AB,P、Q为垂足.求证:DP=DQ.