题目内容
20.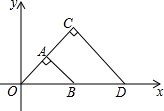 如图,等腰Rt△OAB和等腰Rt△OCD中,∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,若点B的坐标为(1,0),则点C的坐标为( )
如图,等腰Rt△OAB和等腰Rt△OCD中,∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,若点B的坐标为(1,0),则点C的坐标为( )| A. | (1,1) | B. | (2,2) | C. | ($\sqrt{2}$,$\sqrt{2}$) | D. | ($\frac{3}{2}$,$\frac{3}{2}$) |
分析 首先利用等腰直角三角形的性质得出A点坐标,再利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,ky),进而求出即可.
解答 解:∵∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,点B的坐标为(1,0),
∴BO=1,则AO=AB=$\frac{\sqrt{2}}{2}$,
∴A($\frac{1}{2}$,$\frac{1}{2}$),
∵等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,
∴点C的坐标为:(1,1).
故选:A.
点评 此题主要考查了位似变换的性质,正确理解位似与相似的关系,记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
11. 如图,阴影部分在长为a,宽为b的长方形中,当a=10,b=6时,阴影部分的面积是( )
如图,阴影部分在长为a,宽为b的长方形中,当a=10,b=6时,阴影部分的面积是( )
 如图,阴影部分在长为a,宽为b的长方形中,当a=10,b=6时,阴影部分的面积是( )
如图,阴影部分在长为a,宽为b的长方形中,当a=10,b=6时,阴影部分的面积是( )| A. | 8 | B. | 15 | C. | 30 | D. | 60 |
5.某人测得南通市今年10月24日6时到11时的PM2.5的1小时均值(单位:)如下:70,74,78,80,74,75,这组数据的中位数和众数分别是( )
| A. | 79和74 | B. | 74.5和74 | C. | 74和74.5 | D. | 74和79 |
9. 如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D,已知cos∠ACD=$\frac{3}{5}$,BC=5,则AC的长为( )
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D,已知cos∠ACD=$\frac{3}{5}$,BC=5,则AC的长为( )
 如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D,已知cos∠ACD=$\frac{3}{5}$,BC=5,则AC的长为( )
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D,已知cos∠ACD=$\frac{3}{5}$,BC=5,则AC的长为( )| A. | 3 | B. | $\frac{20}{3}$ | C. | 1 | D. | $\frac{16}{3}$ |
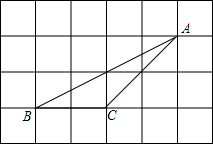 如图,△ABC的顶点都是正方形网格中的格点,则tan∠BAC等于$\frac{1}{3}$.
如图,△ABC的顶点都是正方形网格中的格点,则tan∠BAC等于$\frac{1}{3}$.