题目内容
14.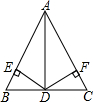 如图,AD是△ABC的中线,DE⊥AB于E,DF⊥AC于F,且BE=CF,求证:AD是△ABC的平分线.
如图,AD是△ABC的中线,DE⊥AB于E,DF⊥AC于F,且BE=CF,求证:AD是△ABC的平分线.
分析 要证AD平分∠BAC,只需证明△EBD≌△FCD,得到DE=DF,利用角平分线的性质的逆定理即可解答.
解答 解:∵AD是△ABC的中线(已知),
∴BD=CD.
在Rt△EBD和Rt△FCD中,
$\left\{\begin{array}{l}{BD=CD}\\{BE=CF}\end{array}\right.$
∴Rt△EBD≌Rt△FCD(HL).
∴DE=DF(全等三角形的对应边相等),
∵DE⊥AB于E,DF⊥AC于F,
∴AD是∠BAC的平分线.
点评 本题考查了全等三角形的判定和性、角平分线的性质,解决本题的关键是证明Rt△EBD≌Rt△FCD.

练习册系列答案
相关题目
3. 如图,方格纸中是9个完全相同的正方形,则∠1+∠2=( )
如图,方格纸中是9个完全相同的正方形,则∠1+∠2=( )
 如图,方格纸中是9个完全相同的正方形,则∠1+∠2=( )
如图,方格纸中是9个完全相同的正方形,则∠1+∠2=( )| A. | 75° | B. | 80° | C. | 90° | D. | 105° |
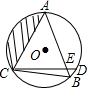 如图,在⊙O中,$\widehat{AD}$=$\widehat{AC}$,弦CD与弦AB交于点E,连接BC,若⊙O的半径长为4cm,∠ACD=60°,求图中阴影部分的面积.
如图,在⊙O中,$\widehat{AD}$=$\widehat{AC}$,弦CD与弦AB交于点E,连接BC,若⊙O的半径长为4cm,∠ACD=60°,求图中阴影部分的面积.