题目内容
5．正十边形的内角和是1440°，其中一个外角是36°．分析 根据多边形内角和定理即可得到正十边形的内角和，再利用正十边形的外角和是360度，并且每个外角都相等，即可求出一个外角的度数，从而得出答案．
解答 解：（10-2）×180°
=8×180°
=1440°，
正十边形的一个外角为360°÷10=36°．
故正十边形的内角和是1440°，其中一个外角是36°．
故答案为：1440°，36°．
点评 本题主要考查了多边形内角和定理：（n-2）•180 （n≥3）且n为整数），正多边形的性质：正多边形的各个外角相等，外角和是360度．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
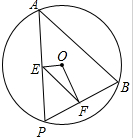如图，点A，B是⊙O上两点，点P是⊙O0上的动点（P与A，B不重合），连接AP，BP，过点O分别作OE⊥AP，OF⊥BP，点E、F分别是垂足．
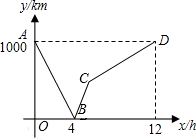一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．下列说法中正确的是③．
如图，在四边形ABCD中，线段BD垂直平分AC，且相交于点0，∠1=∠2，求证：四边形ABCD是菱形．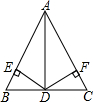
如图，AD是△ABC的中线，DE⊥AB于E，DF⊥AC于F，且BE=CF，求证：AD是△ABC的平分线．
15．反比例函数y=$\frac{{k}^{2}}{x}$（k为常数，k≠0）的图象位于第（ ）象限．
| A． | 一、三 | B． | 二、三 | C． | 一、四 | D． | 二、四 |