题目内容
Rt△ABC≌Rt△DEF,∠ABC=∠DEF=90°,将△ABC和△DEF重叠放置如图①.
(1)保持△ABC不动,将△DEF绕点E顺时针旋转60°,使DF经过点C,如图②.求证:△BCF是等边三角形;
(2)保持△ABC不动,将△DEF绕点E顺时针旋转90°,如图③,判断AC与DF的位置关系,并说明理由.

(1)保持△ABC不动,将△DEF绕点E顺时针旋转60°,使DF经过点C,如图②.求证:△BCF是等边三角形;
(2)保持△ABC不动,将△DEF绕点E顺时针旋转90°,如图③,判断AC与DF的位置关系,并说明理由.

考点:全等三角形的判定与性质,等边三角形的判定
专题:
分析:(1)根据旋转的性质可以得出∠FBC=60°,根据全等三角形的性质可以得出BF=BC,从而得出结论;
(2)延长AC交DF于G,根据全等三角形的性质就可以得出∠D=∠A,可以得出∠D+∠DCG=90°,就可以得出AC⊥DF.
(2)延长AC交DF于G,根据全等三角形的性质就可以得出∠D=∠A,可以得出∠D+∠DCG=90°,就可以得出AC⊥DF.
解答:解:(1)∵Rt△ABC≌Rt△DEF,
∴AB=DE,AC=DF,BC=EF,∠A=∠D.
∵将△DEF绕点E顺时针旋转60°,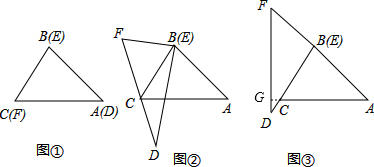
∴∠FBC=60°.
∵BC=BF,
∴△BCF是等边三角形;
(2)AC⊥DF.
理由:延长AC交DF于G,
∵∠ABC=90°,
∴∠A+∠ACB=90°.
∵∠ACB=∠DCG,
∴∠D+∠DCG=90°,
∴∠DGC=90°.
∴AG⊥DF,即AC⊥DF.
∴AB=DE,AC=DF,BC=EF,∠A=∠D.
∵将△DEF绕点E顺时针旋转60°,

∴∠FBC=60°.
∵BC=BF,
∴△BCF是等边三角形;
(2)AC⊥DF.
理由:延长AC交DF于G,
∵∠ABC=90°,
∴∠A+∠ACB=90°.
∵∠ACB=∠DCG,
∴∠D+∠DCG=90°,
∴∠DGC=90°.
∴AG⊥DF,即AC⊥DF.
点评:本题考查了旋转的性质的运用,全等三角形的性质的运用,等边三角形的判定方法的运用,垂直的判定方法的运用,解答时灵活运用全等三角形的性质是关键.

练习册系列答案
相关题目
 如图,已知平行四边形ABCD中,点M是边DC的中点,射线AM、BC相交于点E,设
如图,已知平行四边形ABCD中,点M是边DC的中点,射线AM、BC相交于点E,设| DA |
| a |
| AB |
| b |
| AE |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知抛物线y=x2+3x+c经过三点(
,y1),(-
,y2),(-1,y3),则y1,y2,y3的大小关系为( )
| 2 |
| 3 |
| A、y1>y2>y3 |
| B、y1>y3>y2 |
| C、y2>y1>y3 |
| D、y2>y3>y1 |
 如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长为
如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长为