题目内容
 如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长为
如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长为考点:垂径定理,含30度角的直角三角形,勾股定理
专题:计算题
分析:作OH⊥CD于H,连结OD,由AE=2,EB=6,易得OD=OB=4,则OE=2,在Rt△OHE中根据含30度的直角三角形三边的关系得到OH=
OE=1,再利用勾股定理可计算出DH=
,然后根据垂径定理由OH⊥CD得到CH=DH=
,再利用CD=2DE求解.
| 1 |
| 2 |
| 15 |
| 15 |
解答: 解:作OH⊥CD于H,连结OD,如图,
解:作OH⊥CD于H,连结OD,如图,
∵AE=2,EB=6,
∴直径AB=8,
∴OD=OB=4,
∴OE=OA-AE=2,
在Rt△OHE中,∠DEB=30°,OE=2,
∴OH=
OE=1,
在Rt△OHD中,OD=4,OH=1,
∴DH=
=
,
∵OH⊥CD,
∴CH=DH=
,
∴CD=2
.
故答案为2
.
 解:作OH⊥CD于H,连结OD,如图,
解:作OH⊥CD于H,连结OD,如图,∵AE=2,EB=6,
∴直径AB=8,
∴OD=OB=4,
∴OE=OA-AE=2,
在Rt△OHE中,∠DEB=30°,OE=2,
∴OH=
| 1 |
| 2 |
在Rt△OHD中,OD=4,OH=1,
∴DH=
| OD2-OH2 |
| 15 |
∵OH⊥CD,
∴CH=DH=
| 15 |
∴CD=2
| 15 |
故答案为2
| 15 |
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理以及含30度的直角三角形三边的关系.

练习册系列答案
相关题目
若
=
,则
=( )
| a |
| b |
| 3 |
| 4 |
| a+b |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
下列黑体英文大写字母中不是轴对称图形的是( )
| A、E | B、M | C、N | D、H |

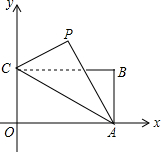 如图,在平面直角坐标系中,矩形OABC的长OA=
如图,在平面直角坐标系中,矩形OABC的长OA=