题目内容
5.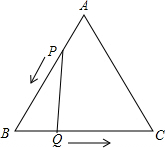 如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,点P的速度都是1cm/s,点Q的速度都是2cm/s当点P到达点B时,P、Q两点停止.当t=$\frac{3}{5}$或$\frac{3}{2}$时,△PBQ是直角三角形.
如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,点P的速度都是1cm/s,点Q的速度都是2cm/s当点P到达点B时,P、Q两点停止.当t=$\frac{3}{5}$或$\frac{3}{2}$时,△PBQ是直角三角形.
分析 先分别表示出BP,BQ的值,当∠BQP和∠BPQ分别为直角时,由等边三角形的性质就可以求出结论.
解答 解:∵△ABC是等边三角形,
∴AB=BC=3cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,∠BPQ=30°,
∴BP=2BQ.
∵BP=3-t,BQ=2t,
∴3-t=2×2t,
解得t=$\frac{3}{5}$;
当∠QPB=90°时,∠PQB=30°,
∴BQ=2PB,
∴2t=2(3-t),
解得t=$\frac{3}{2}$.
答:当t=$\frac{3}{5}$或$\frac{3}{2}$时,△PBQ是直角三角形.
故答案为:$\frac{3}{5}$或$\frac{3}{2}$.
点评 本题考查了等边三角形的性质的运用,30°角的直角三角形的性质的运用,利用分类讨论是解题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目

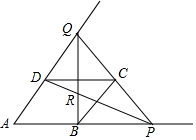 如图,四边形ABCD是边长为a的菱形,且∠A=60°,P是AB延长线上一动点,联结PC并延长交AD的延长线于点Q,联结BQ交PD于点R
如图,四边形ABCD是边长为a的菱形,且∠A=60°,P是AB延长线上一动点,联结PC并延长交AD的延长线于点Q,联结BQ交PD于点R
 如图,弦AB和CD相交于⊙O内一点P,求证:PA•PB=PC•PD.
如图,弦AB和CD相交于⊙O内一点P,求证:PA•PB=PC•PD. 如图,铁道路口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高为8m.(杆的宽度忽略不计)
如图,铁道路口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高为8m.(杆的宽度忽略不计) 如图,已知CF为△ABC的∠ACB的平分线,FD⊥BC,且FD=2cm,BC=7cm,AC=9cm.那么△ABC的面积为16平方厘米.
如图,已知CF为△ABC的∠ACB的平分线,FD⊥BC,且FD=2cm,BC=7cm,AC=9cm.那么△ABC的面积为16平方厘米.