题目内容
13.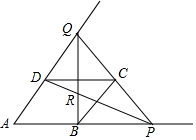 如图,四边形ABCD是边长为a的菱形,且∠A=60°,P是AB延长线上一动点,联结PC并延长交AD的延长线于点Q,联结BQ交PD于点R
如图,四边形ABCD是边长为a的菱形,且∠A=60°,P是AB延长线上一动点,联结PC并延长交AD的延长线于点Q,联结BQ交PD于点R(1)设BP=x,DQ=y,求y与x的函数解析式,并写出定义域;
(2)求∠PRQ的度数.
分析 (1)根据平行线的性质,得出∠DQC=∠BCP,∠QDC=∠CBP=60°,即可得到△QDC∽△PBC,进而得出$\frac{DQ}{BC}=\frac{CD}{PB}$,即$\frac{y}{a}=\frac{a}{x}$,最后得出y与x的函数解析式;
(2)连接BD,根据四边形ABCD是边长为a的菱形,且∠A=60°,得出∠QDB=∠DBP,再根据$\frac{QD}{BD}$=$\frac{a}{x}$,$\frac{BD}{PB}$=$\frac{a}{x}$,即可得到$\frac{QD}{BD}$=$\frac{BD}{PB}$,进而判定∠QDB∽△DBP,从而得出∠BDP=∠DQB,最后根据∠PRQ是△QDR的外角,即可得出∠PRQ=∠DQB+∠QDR=∠BDP+∠QDR=∠BDQ=120.
解答 解:(1)∵四边形ABCD是边长为a的菱形,∠A=60°,
∴CD=BC=a,AD∥BC,∠ADC=∠ABC=120°,
∴∠DQC=∠BCP,∠QDC=∠CBP=60°,
∴△QDC∽△PBC,
∴$\frac{DQ}{BC}=\frac{CD}{PB}$,
即$\frac{y}{a}=\frac{a}{x}$,
∴y=$\frac{{a}^{2}}{x}$(x>0);
(2)连接BD,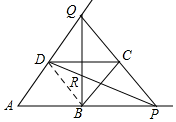
∵四边形ABCD是边长为a的菱形,且∠A=60°,
∴∠ABC=∠ADC=120°,∠ADB=∠ABD=60°,BD=AB=a,
∴∠QDB=180°-∠ADB=120°,∠DBP=180°-∠ABD=120°,
∴∠QDB=∠DBP,
又∵$\frac{QD}{BD}$=$\frac{y}{a}$=$\frac{\frac{{a}^{2}}{x}}{a}$=$\frac{a}{x}$,$\frac{BD}{PB}$=$\frac{a}{x}$,
∴$\frac{QD}{BD}$=$\frac{BD}{PB}$,
∴∠QDB∽△DBP,
∴∠BDP=∠DQB,
∵∠PRQ是△QDR的外角,
∴∠PRQ=∠DQB+∠QDR=∠BDP+∠QDR=∠BDQ=120.
点评 本题主要考查了菱形的性质以及相似三角形的判定与性质的运用,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案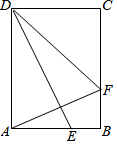 在矩形ABCD中,BC=10cm、DC=6cm,点E、F分别为边AB、BC上的两个动点,E从点A出发以每秒5cm的速度向B运动,F从点B出发以每秒3cm的速度向C运动,设运动时间为t秒.若∠AFD=∠AED,则t的值为( )
在矩形ABCD中,BC=10cm、DC=6cm,点E、F分别为边AB、BC上的两个动点,E从点A出发以每秒5cm的速度向B运动,F从点B出发以每秒3cm的速度向C运动,设运动时间为t秒.若∠AFD=∠AED,则t的值为( )| A. | $\sqrt{2}-1$ | B. | 0.5 | C. | $\frac{2}{3}$ | D. | 1 |
| A. | y2+x=1 | B. | x(x-1)=x2-2 | C. | x2-1=0 | D. | x2+$\frac{1}{x}$=1 |
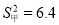 ,乙同学的方差是
,乙同学的方差是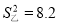 ,那么这两名同学跳高成绩比较稳定的是_____同学.
,那么这两名同学跳高成绩比较稳定的是_____同学. 如图,在△ABC中,∠C=90°,∠A=α,D是边AC上一点,且∠BDC=β,AD=a,求BC的长.(用含a、α、β的式子表示)
如图,在△ABC中,∠C=90°,∠A=α,D是边AC上一点,且∠BDC=β,AD=a,求BC的长.(用含a、α、β的式子表示) 观察图形,利用图形面积关系用写出一个代数恒等式.
观察图形,利用图形面积关系用写出一个代数恒等式.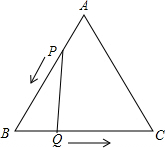 如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,点P的速度都是1cm/s,点Q的速度都是2cm/s当点P到达点B时,P、Q两点停止.当t=$\frac{3}{5}$或$\frac{3}{2}$时,△PBQ是直角三角形.
如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,点P的速度都是1cm/s,点Q的速度都是2cm/s当点P到达点B时,P、Q两点停止.当t=$\frac{3}{5}$或$\frac{3}{2}$时,△PBQ是直角三角形.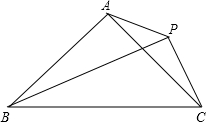 如图,等腰△ABC中,AB=AC,∠BAC=90°,P为△ABC外一点,PA=2$\sqrt{2}$,PB=7,PC=3.
如图,等腰△ABC中,AB=AC,∠BAC=90°,P为△ABC外一点,PA=2$\sqrt{2}$,PB=7,PC=3.