题目内容
3．分解因式：am-3a=a（m-3）．分析 根据提公因式法的一般步骤进行因式分解即可．
解答 解：am-3a=a（m-3）．
故答案为：a（m-3）．
点评 本题考查的是提公因式法进行因式分解，提公因式法基本步骤：找出公因式；提公因式并确定另一个因式：用原多项式除以公因式，所得的商即是提公因式后剩下的一个因式．
练习册系列答案
相关题目
13．计算（-4）+（-9）的结果是（ ）
| A． | -13 | B． | -5 | C． | 5 | D． | 13 |
14．计算（-8）-（-5）的结果等于（ ）
| A． | -3 | B． | -13 | C． | -40 | D． | 3 |
11．（1）计算：（$\frac{1}{3}$）-2-|1-$\sqrt{2}$|+（π-3.14）0+$\frac{1}{2}$$\sqrt{8}$+tan60°
（2）解方程：2x2-3x-3=0．
（2）解方程：2x2-3x-3=0．
18．
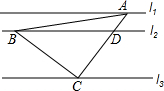如图，直线l1∥l2∥l3，一等腰直角三角形ABC的三个顶点A，B，C分别在l1，l2，l3上，∠ACB=90°，AC交l2于点D，已知l1与l2的距离为1，l2与l3的距离为3，则$\frac{AB}{BD}$的值为（ ）
如图，直线l1∥l2∥l3，一等腰直角三角形ABC的三个顶点A，B，C分别在l1，l2，l3上，∠ACB=90°，AC交l2于点D，已知l1与l2的距离为1，l2与l3的距离为3，则$\frac{AB}{BD}$的值为（ ）| A． | $\frac{4\sqrt{2}}{5}$ | B． | $\frac{\sqrt{34}}{5}$ | C． | $\frac{5\sqrt{2}}{8}$ | D． | $\frac{20\sqrt{2}}{23}$ |
8．甲箱内有4颗球，颜色分别为红、黄、绿、蓝；乙箱内有3颗球，颜色分别为红、黄、黑．小赖打算同时从甲、乙两个箱子中各抽出一颗球，若同一箱中每球被抽出的机会相等，则小赖抽出的两颗球颜色相同的机率为何？（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{6}$ | C． | $\frac{2}{7}$ | D． | $\frac{7}{12}$ |
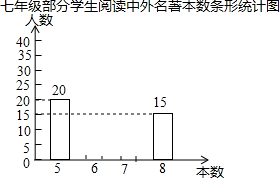为响应“全民阅读”号召，某校在七年级800名学生中随机抽取100名学生，对该年级学生在2015年全年阅读中外名著的情况进行调查，整理调查结果发现，学生阅读中外名著的本数，最少的有5本，最多的有8本，并根据调查结果绘制了如图所示的不完整的条形统计图，其中阅读了6本的人数占被调查人数的30%，根据图中提供的信息，补全条形统计图并估计该校七年级全体学生在2015年全年阅读中外名著的总本数．
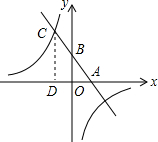已知，如图，一次函数y=kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=$\frac{n}{x}$（n为常数且n≠0）的图象在第二象限交于点C．CD⊥x轴，垂足为D，若OB=2OA=3OD=6．
如图，△ABC内接于⊙O，AH⊥BC于点H，若AC=24，AH=18，⊙O的半径OC=13，则AB=$\frac{39}{2}$．