题目内容
3.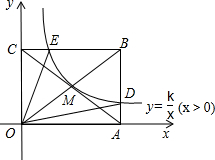 如图,反比例函数$y=\frac{k}{x}({x>0})$的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为12,则k的值为4.
如图,反比例函数$y=\frac{k}{x}({x>0})$的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为12,则k的值为4.
分析 本题可从反比例函数图象上的点E、M、D入手,分别找出△OCE、△OAD、□OABC的面积与|k|的关系,列出等式求出k值.
解答  解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=$\frac{1}{2}$|k|,S△OAD=$\frac{1}{2}$|k|,
解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=$\frac{1}{2}$|k|,S△OAD=$\frac{1}{2}$|k|,
过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,
又∵M为矩形ABCO对角线的交点,则S矩形ABCO=4S□ONMG=4|k|,
由于函数图象在第一象限,
∴k>0,则$\frac{k}{2}$+$\frac{k}{2}$+12=4k,
∴k=4.
点评 本题考查了反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,同学们应高度关注.

练习册系列答案
相关题目
14.下列说法,正确的是( )
| A. | 如果两个数的和为零,那么这两个数一定是一正一负 | |
| B. | -a表示一个负数 | |
| C. | 两个有理数的和一定大于其中每一个加数 | |
| D. | 若-2+x是一个正数,则x一定是正数 |
8.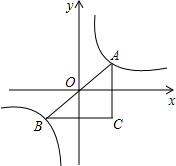 A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点,AC∥y轴,BC∥x轴,则△ABC的面积S为( )
A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点,AC∥y轴,BC∥x轴,则△ABC的面积S为( )
 A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点,AC∥y轴,BC∥x轴,则△ABC的面积S为( )
A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点,AC∥y轴,BC∥x轴,则△ABC的面积S为( )| A. | S=1 | B. | 1<S<2 | C. | S=2 | D. | S>2 |

 如图是一个正方体的表面展开图,则原正方体中“喜”面所对面上的字是数.
如图是一个正方体的表面展开图,则原正方体中“喜”面所对面上的字是数.