题目内容
20. 在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=$\frac{3}{5}$,反比例函数y=$\frac{k}{x}$(k>0)的图象经过AO的中点C且与AB交于点D.
在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=$\frac{3}{5}$,反比例函数y=$\frac{k}{x}$(k>0)的图象经过AO的中点C且与AB交于点D.(1)求k的值;
(2)求点D的坐标;
(3)在x轴上是否存在点P,使得△OCP为等腰三角形?若存在,求出点P的坐标.
分析 (1)过C作x轴的垂线,垂足为点E,由AB也与x轴垂直,得到CE与AB平行,又C为OA的中点,可得出E为OB的中点,即CE为三角形AOB的中位线,在直角三角形AOB中,根据斜边AO的长及sin∠AOB的值,利用锐角三角函数定义求出AB的长,再利用勾股定理求出OB的长,利用三角形中位线定理得到CE等于AB的一半,可得出CE的长,即为C的纵坐标,由OE等于OB的一半,由OB的长求出OE的长,即为点C的横坐标,确定出点C的坐标,将点C的坐标代入到y=$\frac{k}{x}$中,求出k的值,即可确定出反比例函数解析式;
(2)由AB与x轴垂直,且D在AB上,可得出D与B的横坐标相同,由OB的长得出D的横坐标,将求出的D的横坐标代入反比例函数解析式中,求出对应的y的值,即为D的纵坐标,即可确定出D的坐标;
(3)分OC=PC,OC=OP及PC=OP三种情况进行讨论.
解答 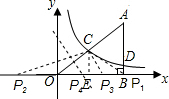 解:(1)过C点作CE⊥OB于E,
解:(1)过C点作CE⊥OB于E,
∵AB⊥OB,CE⊥OB,
∴CE∥AB,又C为OA的中点,
∴E为OB的中点,即CE为△AOB的中位线,
∴CE=$\frac{1}{2}$AB,OE=$\frac{1}{2}$OB,
在Rt△AOB中,AO=10,sin∠AOB=$\frac{3}{5}$,
∴sin∠AOB=$\frac{AB}{AO}$,即AB=10×$\frac{3}{5}$=6,
根据勾股定理得:OB=$\sqrt{{OA}^{2}-{AB}^{2}}$=8,
∴OE=4,CE=3,
∴C的坐标是(4,3),
将C(4,3)代入y=$\frac{k}{x}$中得:k=12,
则反比例函数解析式为y=$\frac{12}{x}$;
(2)∵AB⊥x轴,D在AB上,且OB=8,
∴点D的横坐标为8,
将x=8代入y=$\frac{12}{x}$中得:y=1.5,
∴点D的坐标为(8,1.5);
(3)当OC=PC时,
∵OA=10,CO=5,CE⊥OB,AB⊥OB,
∴CE是△OAB的中线,
∴CE是OB的垂直平分线,
∴点P与点B重合,
∴P1(8,0);
当OC=OP时,
∵OC=5,
∴P2(-5,0),P3(5,0);
当OP=PC时,
∵C(4,3),
∴直线OC的解析式为y=$\frac{3}{4}$x,OC的中点为(2,$\frac{3}{2}$),
∴设线段OC的垂直平分线为y=-$\frac{4}{3}$x+b(k≠0),
∴$\frac{3}{2}$=-$\frac{8}{3}$+b,解得b=$\frac{25}{6}$,
∴此直线的解析式为y=-$\frac{4}{3}$x+$\frac{25}{6}$,
∴当y=0时,x=$\frac{25}{8}$,
∴P4($\frac{25}{8}$,0).
综上所述,P1(8,0),P2(-5,0),P3(5,0),P4($\frac{25}{8}$,0).
点评 本题考查的是反比例函数综合题,在解答(1)时要作出辅助线,构造出三角形的中位线,利用勾股定理求解,在解答(3)时要进行分类讨论,不要漏解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 型 号 | A | B |
| 进价(元/件) | 120 | 100 |
| 售价(元/件) | 135 | 120 |
(2)该果商第二次以原价购进A、B两种血脐,购进B种血脐的件数不变,而购进A种血脐的件数是第一次的2倍,A种血脐按原价销售,而B种血脐打折销售,若两种血脐销售完毕,要使得第二次经营活动或利润不少于7500元,求B种血脐最低售价是多少?
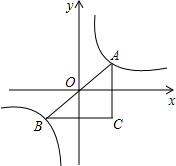 A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点,AC∥y轴,BC∥x轴,则△ABC的面积S为( )
A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点,AC∥y轴,BC∥x轴,则△ABC的面积S为( )| A. | S=1 | B. | 1<S<2 | C. | S=2 | D. | S>2 |
 如图是一个正方体的表面展开图,则原正方体中“喜”面所对面上的字是数.
如图是一个正方体的表面展开图,则原正方体中“喜”面所对面上的字是数.
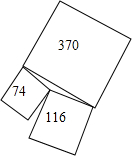 如图,三个正方形形状的土地面积分别为74英亩,116英亩,370英亩,三个正方形恰好围着一个池塘.现要将这550英亩的土地拍卖,如果有人能计算出池塘的面积,那么池塘不计入土地价钱白白奉送,英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解答吗?
如图,三个正方形形状的土地面积分别为74英亩,116英亩,370英亩,三个正方形恰好围着一个池塘.现要将这550英亩的土地拍卖,如果有人能计算出池塘的面积,那么池塘不计入土地价钱白白奉送,英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解答吗?