题目内容
18．先用配方法说明2x2-4x+7的值总大于0，在求出当x为何值时，代数式2x2-4x+7的值最小，最小值是多少．分析 先利用配方法得到2x2-4x+7=2（x-1）2+5，再根据非负数的性质即可得到代数式2x2-4x+7的值都大于零；并且当（x-1）2=0，即x=1时，代数式2x2-4x+7有最小值．
解答 解：2x2-4x+7
=2x2-4x+2+5
=2（x-1）2+5，
∵（x-1）2≥0，
∴2（x-1）2+5＞0，
∴代数式2x2-4x+7的值都大于零；
当（x-1）2=0，即x=1时，代数式2x2-4x+7有最小值，最小值为5．
点评 本题考查了配方法的应用：配方法的理论依据是公式a2±2ab+b2=（a±b）2．二次三项式是完全平方式，则常数项是一次项系数一半的平方．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
8．
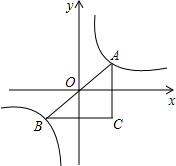A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点，AC∥y轴，BC∥x轴，则△ABC的面积S为（ ）
A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点，AC∥y轴，BC∥x轴，则△ABC的面积S为（ ）| A． | S=1 | B． | 1＜S＜2 | C． | S=2 | D． | S＞2 |
如图，A（4，0），B（0，4）两点，P在BA延长线上，△OPE为等腰直角三角形，F为PE的中点，OF交AB于M．