题目内容
14.某商场购进一种单价为40元的书包,如果以单价50元出售,那么每月可售出30个,根据销售经验,售价每提高5元,销售量相应减少1个.(1)请写出销售单价提高x元与总的销售利润y元之间的函数关系式;
(2)如果你是经理,为使每月的销售利润最大,那么你确定这种书包的单价为多少元?此时,最大利润是多少元?
分析 (1)根据题意可以求得销售单价提高x元与总的销售利润y元之间的函数关系式;
(2)将(1)中的函数解析式化为顶点式即可解答本题.
解答 解:(1)由题意可得,
y=(50+x-40)(30-$\frac{x}{5}$)=$-\frac{1}{5}{x}^{2}+28x+300$,
即销售单价提高x元与总的销售利润y元之间的函数关系式y=$-\frac{1}{5}{x}^{2}+28x+300$(0≤x≤150);
(2)∵y=$-\frac{1}{5}{x}^{2}+28x+300$=$-\frac{1}{5}(x-70)^{2}+1280$,
∴当x=70时,y取得最大值,此时y=1280,
即为使每月的销售利润最大,这种书包的单价为70元,此时,最大利润是1280元.
点评 本题考查二次函数的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用二次函数的顶点式求函数的最值,注意自变量的取值范围.

练习册系列答案
相关题目
2.已知A(-1,y1)、B(2,y2)、C(-3,y3)在函数y=-2(x+1)2+3的图象上,则y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y2<y3<y1 | D. | y3<y2<y1 |
6.已知代数式4x-12+8y的值是8,则代数式x+2y的值是( )
| A. | 5 | B. | 20 | C. | -1 | D. | 2 |
 如图,在Rt△ABC中,∠C=90°,D是AC中点,DE⊥AB于E,若AE=2$\sqrt{5}$,BC=5,则BE=3$\sqrt{5}$.
如图,在Rt△ABC中,∠C=90°,D是AC中点,DE⊥AB于E,若AE=2$\sqrt{5}$,BC=5,则BE=3$\sqrt{5}$.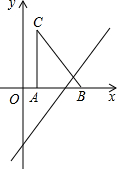 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).