题目内容
15.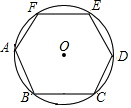 正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )
正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 连接OA,OB,根据等边三角形的性质可得⊙O的半径,进而可得出结论.
解答  解:连接OB,OC,
解:连接OB,OC,
∵多边形ABCDEF是正六边形,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OB=BC,
∵正六边形的周长是12,
∴BC=2,
∴⊙O的半径是2,
故选B.
点评 本题考查的是正多边形和圆,熟知正六边形的性质是解答此题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
6. 一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
 一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
10.如图1,菱形纸片ABCD的边长为2,∠ABC=60°,将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P(如图2),则六边形AEFCHG面积的最大值是( )
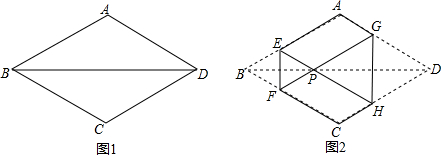

| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | 2-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
20.计算:(2x2)3-6x3(x3+2x2+x)=( )
| A. | -12x5-6x4 | B. | 2x6+12x5+6x4 | C. | x2-6x-3 | D. | 2x6-12x5-6x4 |
4.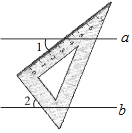 已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )
已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )
 已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )
已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )| A. | 37° | B. | 53° | C. | 63° | D. | 27° |
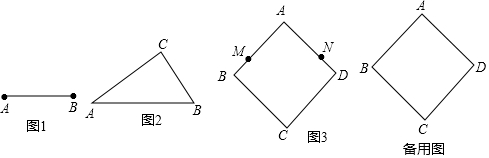
5.下列4个图案中,是轴对称图形的个数为( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,已知AB⊥BC,BD⊥AC,EC⊥AC,∠1与∠2互补,试说明DF⊥BC的理由.
如图,已知AB⊥BC,BD⊥AC,EC⊥AC,∠1与∠2互补,试说明DF⊥BC的理由.