题目内容
3.为了了解某校九年级学生的体能情况,随机抽取部分学生进行体能测试,成绩分别记为A、B、C、D共四个等级,其中A级和B级成绩都评为“优”,将测试结果绘制成如下条形统计图和扇形统计图.(1)求抽取参加体能测试的学生人数,并求出其中C级占有的学生人数;
(2)若该校九年级学生有1000人,则体能测试成绩评为“优”的学生共有几人?
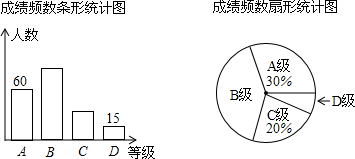
分析 (1)根据统计图中A级有60人,占30%,即可求得本次抽取的学生数,然后根据C级占的百分比即可求得C级占有的学生数;
(2)根据(1)中的答案和统计图中的数据可以求得B级学生数,从而可以求得体能测试成绩评为“优”的学生共有的学生数.
解答 解:(1)由题意可得,
抽取参加体能测试的学生有:60÷30%=200(人),
C级占有的学生人有:600×20%=40(人),
答:抽取参加体能测试的学生有200人,其中C级占有的学生人有40人;
(2)由题意可得,
抽取的学生B级有:200-60-40-15=85(人),
∴体能测试成绩评为“优”的学生共有:1000×$\frac{60+85}{200}$=725(人),
答:体能测试成绩评为“优”的学生共有725人.
点评 本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用统计图中的数据和数形结合的思想解答.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
13.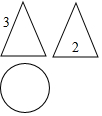 如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的侧面积为( )cm2.
如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的侧面积为( )cm2.
 如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的侧面积为( )cm2.
如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的侧面积为( )cm2.| A. | 3π | B. | 6π | C. | 9π | D. | 12π |
14.下列各数中是无理数的是( )
| A. | 3.14 | B. | $\sqrt{16}$ | C. | $\frac{2}{3}$ | D. | $\sqrt{6}$ |
11. 如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD为( )
如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD为( )
 如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD为( )
如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD为( )| A. | 30° | B. | 50° | C. | 60° | D. | 70° |
18.已知一列数:1,-2,3,-4,5,-6,7,…将这列数排成下列形式:
第1行 1
第2行-2 3
第3行-4 5-6
第4行 7-8 9-10
第5行 11-12 13-14 15
…
按照上述规律排下去,那么第100行从左边数第5个数是( )
第1行 1
第2行-2 3
第3行-4 5-6
第4行 7-8 9-10
第5行 11-12 13-14 15
…
按照上述规律排下去,那么第100行从左边数第5个数是( )
| A. | -4955 | B. | 4955 | C. | -4950 | D. | 4950 |
8.用反证法证明“若a⊥c,b⊥c,则a∥b”时,第一步应先假设( )
| A. | a不垂直于c | B. | b不垂直于c | C. | c不平行于b | D. | a不平行于b |
15.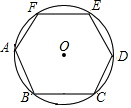 正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )
正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )
 正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )
正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
12.为了解某市参加中考的32000名学生的视力情况,抽查了其中1600名学生的视力进行统计分析,下面叙述正确的是( )
| A. | 32000名学生是总体 | |
| B. | 1600名学生的视力是总体的一个样本 | |
| C. | 每名学生是总体的一个样本 | |
| D. | 以上调査是全面调查 |
