题目内容
6.如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.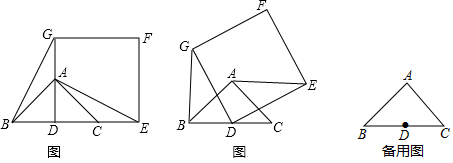
(1)求证:AE=BG
(2)将正方形DEFG绕点D逆时针方向旋转α(0°<α≤360°)如图2所示,判断(1)中的结论是否仍然成立?如果仍成立,请给予证明;如果不成立,请说明理由;
(3)若BC=DE=4,当旋转角α为多少度时,AE取得最大值?直接写出AE取得最大值时α的度数,并利用备用图画出这时的正方形DEFG,最后求出这时AF的值.
分析 (1)在Rt△BDG与Rt△EDA;根据边角边定理易得Rt△BDG≌Rt△EDA;故BG=AE;
(2)连接AD,根据直角三角形与正方形的性质可得Rt△BDG≌Rt△EDA;进而可得BG=AE;
(3)根据(2)的结论,求BG的最大值,分析可得此时F的位置,由勾股定理可得答案.
解答 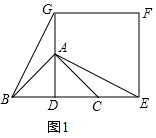 (1)证明:∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,
(1)证明:∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,
∴AD⊥BC,BD=CD,
∴∠ADB=∠ADC=90°,AD=DC=DB,
∵四边形DEFG是正方形,
∴DE=DG,
∴△ADE≌△BDG(SAS),
∴BG=AE;
(2)成立;
理由如下:如图2,连接AD,
由(1)知AD=BD,AD⊥BC.
∴∠ADG+∠GDB=90°.
∵四边形EFGD为正方形,
∴DE=DG,且∠GDE=90°.
∴∠ADG+∠ADE=90°
∴∠BDG=∠ADE.
在△BDG和△ADE中,
∵BD=AD,∠BDG=∠ADE,GD=ED,
∴△BDG≌△ADE(SAS)
∴AE=BG;
(3)α=270°;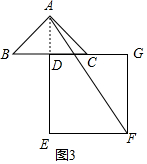
正方形DEFG如图3所示
由(2)知BG=AE
∴当BG取得最大值时,AE取得最大值.
∵BC=DE=4,
∴EF=4,
∴BG=2+4=6
∴AE=6
在Rt△AEF中,由勾股定理,得
AF=$\sqrt{A{E}^{2}+E{F}^{2}}$=$\sqrt{36+16}$=2$\sqrt{13}$.
点评 解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,搞清楚矩形、菱形、正方形中的三角形的三边关系,可有助于提高解题速度和准确率.

练习册系列答案
相关题目
17.在实数-2,$\sqrt{2}$,0,-1中,最小的数是( )
| A. | -2 | B. | $\sqrt{2}$ | C. | 0 | D. | -1 |
11.估计$\frac{\sqrt{5}-1}{2}$介于( )
| A. | 0.6与0.7之间 | B. | 0.7与0.8之间 | C. | 0.8与0.9之间 | D. | 0.9与1之间 |
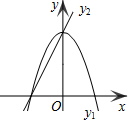 如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断: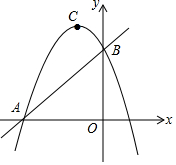 如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B,抛物线的顶点为C.
如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B,抛物线的顶点为C.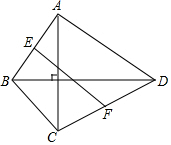 在四边形ABCD中,对角线AC⊥BD且AC=4、BD=6.E、F分别是边AB、CD的中点,则EF=$\sqrt{13}$.
在四边形ABCD中,对角线AC⊥BD且AC=4、BD=6.E、F分别是边AB、CD的中点,则EF=$\sqrt{13}$.