题目内容
8．用计算器计算可以发现：$\sqrt{121}=11，\sqrt{12321}=111，\sqrt{1234321}$=1111，…，由此可得$\sqrt{12345678987654321}$=111111111．分析 利用二次根式的性质结合数字变化规律化简求出即可．
解答 解：∵$\sqrt{121}=11，\sqrt{12321}=111，\sqrt{1234321}$=1111，…，
∴由此可得$\sqrt{12345678987654321}$=111111111．
故答案为：111111111．
点评 此题主要考查了二次根式的化简，正确利用已知发现数字变化规律是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
已知反比例函数y=$\frac{k}{x}$的图象如图，则函数y=kx-2的图象是图中的（ ）
3．下列说法错误的是（ ）
| A． | 一组数据的平均数、众数、中位数可能是同一个数 | |
| B． | 一组数据中中位数可能不唯一确定 | |
| C． | 一组数据中平均数、众数、中位数是从不同角度描述了一组数据的集中趋势 | |
| D． | 一组数据中众数可能有多个 |
20．
如图，△ABC的三个顶点分别在正方形网格的格点上，则tanC的值是（ ）
如图，△ABC的三个顶点分别在正方形网格的格点上，则tanC的值是（ ）| A． | $\frac{6}{5}$ | B． | $\frac{2\sqrt{10}}{3}$ | C． | $\frac{5}{6}$ | D． | $\frac{3\sqrt{10}}{3}$ |
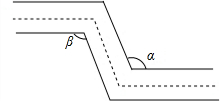如图，是一条暖气管道的剖面图，如果要求管道拐弯前后的方向保持不变，那么管道的两个拐角∠α与∠β之间应该满足的关系是，理由是内错角相等，两直线平行．