Question

18．如图，在△ABC中，∠BAC=90°，AB=AC，分别过点B、C两点作过点A的直线的垂线，垂足为M、N
（1）如图1，当M、N两点在直线BC的同侧时，求证：BM+CN=MN；
（2）如图2，当M、N两点在直线BC的两侧时，BM、CN、MN三条线段的数量关系并证明．

Answer 1

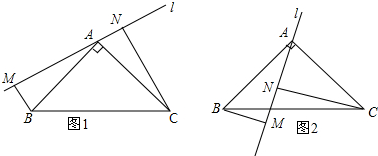
分析 （1）由垂线的定义和角的互余关系得出∠AMB=∠CNA=90°，∠ABM=∠CAN，由AAS证明△ABM≌△CAN，得出对应边相等BM=AN，AM=CN，由AN+AM=MN，即可得出结论；
（2）由垂线的定义和角的互余关系得出∠AMB=∠BNA=90°，∠ABM=∠CAN，由AAS证明△ABM≌△CAN，得出对应边相等BM=AN，AM=CN，由AN+MN=AM，即可得出结论．

解答 （1）证明：∵∠BAC=90°，
∴∠BAM+∠CAN=90°，
∵BM⊥l，BN⊥l，
∴∠AMB=∠CNA=90°，
∴∠BAM+∠ABM=90°，
∴∠ABM=∠CAN，
在△ABM和△CAN中，$\left\{\begin{array}{l}{∠AMB=∠BNA}&{\;}\\{∠ABM=∠CAN}&{\;}\\{AB=AC}&{\;}\end{array}\right.$，
∴△ABM≌△CAN（AAS），
∴BM=AN，AM=CN，
∵AN+AM=MN，
∴BM+CN=MN；
（2）解：BM+MN=CN；理由如下：
∵∠BAC=90°，
∴∠BAM+∠CAN=90°，
∵BM⊥l，BN⊥l，
∴∠AMB=∠BNA=90°，
∴∠BAM+∠ABM=90°，
∴∠ABM=∠CAN，
在△ABM和△CAN中，$\left\{\begin{array}{l}{∠AMB=∠BNA}&{\;}\\{∠ABM=∠CAN}&{\;}\\{AB=AC}&{\;}\end{array}\right.$，
∴△ABM≌△CAN（AAS），
∴BM=AN，AM=CN，
∵AN+MN=AM，
∴BM+MN=CN．

点评 本题考查了全等三角形的判定与性质、垂线的定义、角的互余关系；熟练掌握全等三角形的判定与性质，并能进行推理论证是解决问题的关键．