题目内容
4.已知直线y=kx+b,若点C(m,n),点D(p,q)(其中m<p)都在直线y=kx+b上,且m+p=2,n+q=b2+4b+2,试比较n和q的大小,并说明理由.分析 由点C、点D在直线y=kx+b上,可以得出n与m的关系以及q与p的关系,结合“m+p=2,n+q=b2+4b+2”可得出2k=b2+2b+2=(b+1)2+1≥1,由k>0即可得知y=kx+b为增函数,结合m<p即可得出结论.
解答 解:n<q,理由如下:
∵点C(m,n),点D(p,q)在直线y=kx+b,
∴有$\left\{\begin{array}{l}{n=km+b}\\{q=kp+b}\end{array}\right.$,
∴n+q=k(m+p)+2b,
又∵m+p=2,n+q=b2+4b+2,
∴2k+2b=b2+4b+2,即2k=b2+2b+2=(b+1)2+1≥1,
∴k>0,即y=kx+b为增函数.
∵m<p,
∴n<q.
点评 本题考查了一次函数图象上点的坐标特征,解题的关键是找出一次函数一次项系数k>0.本题属于基础题,难度不大,解决该题型题目时,由点在直线上找出点的横纵坐标之间的关系,结合给定的条件想办法找出一次函数一次项系数的正负值是关键.

练习册系列答案
相关题目
15.为了解我区七年级6000名学生期中数学考试情况,从中抽取了500名学生的数学成绩进行统计.下列判断:
①这种调查方式是抽样调查;
②6000名学生是总体;
③每名学生的数学成绩是个体;
④500名学生是总体的一个样本.
其中正确的判断有( )
①这种调查方式是抽样调查;
②6000名学生是总体;
③每名学生的数学成绩是个体;
④500名学生是总体的一个样本.
其中正确的判断有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.如表列出了皮球反弹高度和下落高度的数据,其中d表示皮球的下落高度,h表示皮球落地后的反弹高度(单位:cm)
(1)表中反映了哪两个变量之间的关系?哪个是自变量?哪个是函数?
(2)当下落高度是100cm时,皮球的反弹高度是多少?
(2)预测下落高度是90cm时,皮球的反弹高度是多少?
| d | 50 | 80 | 100 | 150 |
| h | 25 | 40 | 50 | 75 |
(2)当下落高度是100cm时,皮球的反弹高度是多少?
(2)预测下落高度是90cm时,皮球的反弹高度是多少?
19.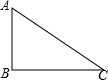 如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
 如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )| A. | 相交 | B. | 相离 | C. | 相切 | D. | 不能确定 |
16. 如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
 如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | 2 | B. | 2$\sqrt{6}$ | C. | 3 | D. | 4 |
14.计算:$\frac{4}{{x}^{2}-4}$-$\frac{1}{x-2}$的正确结果是( )
| A. | -$\frac{1}{x+2}$ | B. | 1-x | C. | 1 | D. | -1 |