Question

3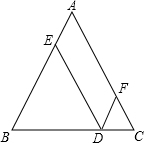．如图，在△ABC中，AB=AC=10，点D在BC上，DE∥AC交AB于E，DF∥AB交AC于F，求：四边形AEDF的周长．

Answer 1

分析 根据等角对等边可证明ED=FC，先根据等腰三角形的性质和平行的性质得到∠EDC=∠C，再证明ED=FC；根据平行四边形的性质可知：平行四边形的周长正好是AC的2倍，即C_?AEDF=2AC=20．

解答 解：∵AB=AC，
∴∠B=∠C，
∵DF∥AB，
∴∠FDC=∠B，
∴∠FDC=∠C，
∴FD=FC，
∵DE∥AC，DF∥AB，
∴四边形AEDF是平行四边形．
∴C_?AEDF=2AC=20．

点评 主要考查了等腰三角形的性质和平行四边形的性质．要掌握等腰三角形的性质：两个底角相等，三角形内角和为180度．会熟练运用等边对等角或等角对等边．