题目内容
15.已知y=x-4的图象与x轴交于点A,与y=kx+b的图象交于点C,点C的横坐标是5,直线y=kx+b与x轴交于点B,且S△ABC=$\frac{5}{2}$,求直线y=kx+b的解析式.分析 先求出A、C两点的坐标,再用k、b表示出B点坐标,再利用三角形的面积公式即可得出结论.
解答 解:∵y=x-4的图象与x轴交于点A,
∴A(4,0).
∵点C的横坐标是5,
∴C(5,1),
∴5k+b=1,即b=1-5k.
∵直线y=kx+b与x轴交于点B,
∴B(-$\frac{b}{k}$,0).
∵S△ABC=$\frac{5}{2}$,
∴$\frac{1}{2}$BC•1=$\frac{5}{2}$,即$\frac{1}{2}$|4+$\frac{b}{k}$|=$\frac{5}{2}$,
∴|4+$\frac{1-5k}{k}$|=5,解得k=$\frac{1}{6}$或k=-$\frac{1}{4}$,
当k=$\frac{1}{6}$时,b=1-$\frac{5}{6}$=$\frac{1}{6}$,此时直线y=kx+b的解析式为y=$\frac{1}{6}$x+$\frac{1}{6}$;
当k=-$\frac{1}{4}$时,b=1+$\frac{5}{4}$=$\frac{9}{4}$,此时直线y=kx+b的解析式为y=-$\frac{1}{4}$x+$\frac{9}{4}$;
综上所述,直线y=kx+b的解析式为y=$\frac{1}{6}$x+$\frac{1}{6}$或y=-$\frac{1}{4}$x+$\frac{9}{4}$.
点评 本题考查的是待定系数法求一次函数的解析式,在解答此题时要注意进行分类讨论.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
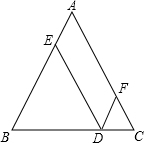 如图,在△ABC中,AB=AC=10,点D在BC上,DE∥AC交AB于E,DF∥AB交AC于F,求:四边形AEDF的周长.
如图,在△ABC中,AB=AC=10,点D在BC上,DE∥AC交AB于E,DF∥AB交AC于F,求:四边形AEDF的周长.