Question

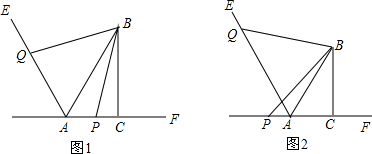
16．如图，以△ABC三边向外作三个正方形，O₁，O₂，O₃为相应正方形的中心，求证：AO₃=O₁O₂，且AO₃⊥O₁O₂．

Answer 1

分析 作O₂E⊥AC、O₃D⊥BC证△PDO₃≌△PEO₂得PO₂=PO₃、∠PO₂E=∠DPO₃，进而可推得∠O₁PO₂=∠APO₃；再证△O₁PO₂≌△APO₃可知AO₃=O₁O₂、∠PO₁O₂=∠PAO₃，根据∠PO₁O₂+∠PHO₁=90°、∠PHO₁=∠AHO₂易知O₁O₂⊥AO₃．

解答 证明：如图，分别过O₂、O₃作O₂E⊥AC，O₃D⊥BC，连接PD、PE，记O₁O₂与AO₃交点为H，PO₂与AC交点为G，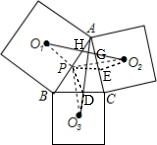

∵O₁，O₂，O₃为相应正方形的中心，
∴AE=CE=EO₂=$\frac{1}{2}$AC，O₃D=CD=BD=$\frac{1}{2}$BC，∠BDO₃=∠AEO₂=90°
∵P、D、E均为中点，
∴PD、PE均为△ABC的中位线，
∴PD=$\frac{1}{2}$AC=O₂E，PD∥AC，PE=$\frac{1}{2}$BC=O₃D，PE∥BC，
∴∠BDP=∠BCA=∠PEA，
∴∠PDO₃=∠PEO₂，
在△PDO₃和△PEO₂中，
$\left\{\begin{array}{l}{PD={O}_{2}E}\\{∠PD{O}_{3}=∠PE{O}_{2}}\\{D{O}_{3}=PE}\end{array}\right.$，
∴△PDO₃≌△PEO₂（SAS），
∴PO₂=PO₃，∠PO₂E=∠DPO₃，
∵∠O₂GE+∠PO₂E=90°，∠O₂GE=∠GPD，
∴∠O₃PD+∠GPD=90°，即∠O₃PO₂=90°，
又∵∠O₁PO₂=∠O₁PA+∠APO₂=90°+∠APO₂，∠APO₃=∠O₃PO₂+∠APO₂=90°+∠APO₂，
∴∠O₁PO₂=∠APO₃，
在△O₁PO₂和△APO₃中，
$\left\{\begin{array}{l}{{O}_{1}P=AP}\\{∠{O}_{1}P{O}_{2}=∠AP{O}_{3}}\\{P{O}_{2}=P{O}_{3}}\end{array}\right.$，
∴△O₁PO₂≌△APO₃（SAS），
∴AO₃=O₁O₂，∠PO₁O₂=∠PAO₃，
又∵∠PO₁O₂+∠PHO₁=90°，且∠PHO₁=∠AHO₂，
∴∠PAO₃+∠AHO₂=90°，
∴O₁O₂⊥AO₃，
故O₁O₂=AO₃，且O₁O₂⊥AO₃．

点评 本题主要考查全等三角形判定和性质及三角形中位线定理，通过构建△PDO₃≌△PEO₂来证明△O₁PO₂≌△APO₃是解题关键．