题目内容
9. 如图,已知△ABC中,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.求证:△ACF∽△BEC.
如图,已知△ABC中,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.求证:△ACF∽△BEC.
分析 可证明∠A=∠B=45°,再根据外角的性质和已知条件可得出∠ACF=∠BEC,则△ACF∽△BEC.
解答 证明:∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∴∠BEC=∠ACE+∠A=∠ACE+45°,
∵∠ECF=45°,
∴∠ACF=∠ACE+45°,
∴△ACF∽△BEC.
点评 本题考查了相似三角形的判定方法:
(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;
(2)三边法:三组对应边的比相等的两个三角形相似;
(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
(4)两角法:有两组角对应相等的两个三角形相似.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
19.下列各式中运算正确的是( )
| A. | 3a-4a=-1 | B. | a2+a2=a4 | C. | 3a2+2a3=5a5 | D. | 5a2b-6a2b=-a2b |
20.下列四个实数中,是无理数的为( )
| A. | 0 | B. | 0.102002 | C. | 0.202002… | D. | $\frac{2}{7}$ |
1.已知|x|=5,|y|=2,且x<y,则x+y的值( )
| A. | 7 | B. | 3 | C. | -3或3 | D. | -3或-7 |
 如图,起重机吊运物体,∠ABC=90°.若BC=5m,AC=13m,则AB=12m.
如图,起重机吊运物体,∠ABC=90°.若BC=5m,AC=13m,则AB=12m.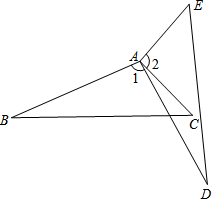 已知:如图,∠B=∠D,∠1=∠2,AB=AD.求证:AC=AE.
已知:如图,∠B=∠D,∠1=∠2,AB=AD.求证:AC=AE. 如图,已知抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;
如图,已知抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;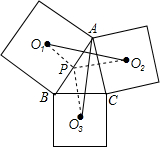 如图,以△ABC三边向外作三个正方形,O1,O2,O3为相应正方形的中心,求证:AO3=O1O2,且AO3⊥O1O2.
如图,以△ABC三边向外作三个正方形,O1,O2,O3为相应正方形的中心,求证:AO3=O1O2,且AO3⊥O1O2.