题目内容
4. 已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CE⊥AD于E,交AB于F.连接DF.求证:∠ADC=∠BDF.
已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CE⊥AD于E,交AB于F.连接DF.求证:∠ADC=∠BDF.
分析 作CH⊥AB于H,交AD于G,根据等腰直角三角形的性质得到∠ACH=∠BCH=45°,即∠ACG=45°,∠B=45°,由CE⊥AD,根据等角的余角相等得到∠1=∠2,则可根据“ASA”判断△AGC≌△CFB,得到CG=BF,然后根据“SAS”证明△CGD≌△BFD,则可得到∠CDA=∠FDB
解答 解:作CH⊥AB于H,交AD于G,连接BE,如图,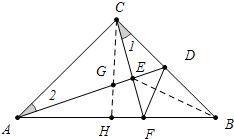
∵△ABC为等腰直角三角形,
∴∠ACH=∠BCH=45°,即∠ACG=45°,∠B=45°
∵CE⊥AD,
∴∠1+∠ACE=∠2+∠ACE=90°,
∴∠1=∠2,
在△AGC和△CFB中,
$\left\{\begin{array}{l}{∠1=∠2}\\{AC=CB}\\{∠ACG=∠CBF}\end{array}\right.$,
∴△AGC≌△CFB(ASA),
∴CG=BF,
∵AD为腰CB上的中线,
∴CD=BD,
在△CGD和△BFD中,
$\left\{\begin{array}{l}{CG=BF}\\{∠GCD=∠B}\\{CD=BD}\end{array}\right.$,
∴△CGD≌△BFD(SAS),
∴∠CDA=∠FDB.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质;本题有一定难度,需要通过作辅助线两次证明三角形全等才能得出结论.

练习册系列答案
相关题目
 如图,起重机吊运物体,∠ABC=90°.若BC=5m,AC=13m,则AB=12m.
如图,起重机吊运物体,∠ABC=90°.若BC=5m,AC=13m,则AB=12m. 如图,已知抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;
如图,已知抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2; 如图,△ABC和△CDE都是等边三角形,试说明∠AEB-∠EBD=60°.
如图,△ABC和△CDE都是等边三角形,试说明∠AEB-∠EBD=60°.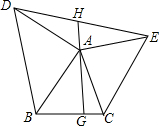 如图,在△ABC中,以A为顶点,以AB、AC为直角三角形的直角边向外侧作等腰直角三角形,连接DE,过A点向BC作垂线AG.反向延长AG交DE于H.
如图,在△ABC中,以A为顶点,以AB、AC为直角三角形的直角边向外侧作等腰直角三角形,连接DE,过A点向BC作垂线AG.反向延长AG交DE于H. 如图,已知CD,BE相交于点A,M是BC的中点,∠1=∠2,∠3=∠4,求证:BD=EC.
如图,已知CD,BE相交于点A,M是BC的中点,∠1=∠2,∠3=∠4,求证:BD=EC.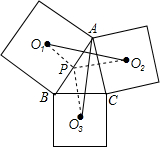 如图,以△ABC三边向外作三个正方形,O1,O2,O3为相应正方形的中心,求证:AO3=O1O2,且AO3⊥O1O2.
如图,以△ABC三边向外作三个正方形,O1,O2,O3为相应正方形的中心,求证:AO3=O1O2,且AO3⊥O1O2.