��Ŀ����
2����֪����ͼ1��ֱ��y=-x-1�ֱ�x�ᡢy����A��E���㣬������y=-$\frac{4}{9}$x2+bx+c������A���ҹ���B��5��0������y�ύ�ڵ�C����DΪ�����ߵĶ��㣬����BC����1���������ߵĽ���ʽ������D�����ꣻ
��2����ͼ2������ֱ��BC�Ϸ�������������һ��F������BCF��������ʱ����һ�߶�MN=$\sqrt{2}$����M�ڵ�N����ࣩ��ֱ��AE���ƶ�����β˳�����ӵ�F��M��N��B�����ı���FMNB��������ı���FMNB���ܳ���Сʱ��M�ĺ����ꣻ
��3����ͼ3������AD��BD���ѡ�DAB��x��ƽ�Ƶ���D��A��B�䣬��ƽ�ƹ����аѡ�D��A��B����A����ת��ʹ��D��A��B���һ��ʼ�վ�����D����һ�߽�ֱ��BD�ڵ�R���Ƿ���������ĵ�R��ʹ��DRA��Ϊ���������Σ������ڣ����BR�ij����������ڣ�˵�����ɣ�
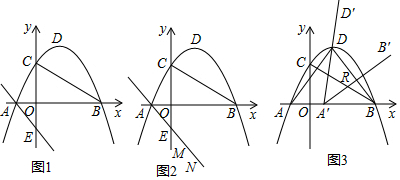
���� ��1�������A���꣬���ɴ���ϵ�����������ƽ���ĵĽ���ʽ���������䷽��������������ߵĶ������꣮
��2����ͼ1�У���F��m��-$\frac{4}{9}$m2+$\frac{16}{9}$m+$\frac{20}{9}$������FH��OC��BC��H���������κ��������ɶ��κ��������ʼ��������F�����꣬��FG��MN��ʹ��FG=MN������GN����G����ֱ��MN�ĶԳƵ�P������BP��AE��N����ʱ�ı���FMNB���ܳ���̣������P�����꣬�Լ�ֱ��PB�Ľ���ʽ�����÷����鼴�������N�����꣬�ѵ�N����ƽ��1����λ��������ƽ��һ����λ�ɵ�M���ɴ˼��ɽ�����⣮
��3������������������ͼ2�У���A��D=A��Bʱ����֤��ADA��ա�BA��R������AD=BA�䣬AA��=BR������ͼ3�У���RD=RA��ʱ����RG��AD��G����취�������̼��ɽ�����⣮
��� �⣺��1����ֱ��y=-x-1�ֱ�x�ᡢy����A��E���㣬
��A��-1��0����E��0��-1����
��A��-1��0����B��5��0������y=-$\frac{4}{9}$x2+bx+c�õ�$\left\{\begin{array}{l}{-\frac{4}{9}-b+c=0}\\{-\frac{100}{9}+5b+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=\frac{16}{9}}\\{c=\frac{20}{9}}\end{array}\right.$��
�������ߵĽ���ʽΪy=-$\frac{4}{9}$x2+$\frac{16}{9}$x+$\frac{20}{9}$��
��y=-$\frac{4}{9}$x2+$\frac{16}{9}$x+$\frac{20}{9}$=-$\frac{4}{9}$��x-2��2+4��
�������߶���D���꣨2��4����
��2����ͼ1�У���F��m��-$\frac{4}{9}$m2+$\frac{16}{9}$m+$\frac{20}{9}$������FH��OC��BC��H��
��B��5��0����C��0��$\frac{20}{9}$����
��ֱ��BC�Ľ���ʽΪy=-$\frac{4}{9}$x+$\frac{20}{9}$����H��m��-$\frac{4}{9}$m+$\frac{20}{9}$����FH=-$\frac{4}{9}$m2+$\frac{20}{9}$m��
��S��BCF=$\frac{1}{2}$•FH•5=-$\frac{10}{9}$��m-$\frac{5}{2}$��2+$\frac{125}{18}$��
��-$\frac{10}{9}$��0��
��m=$\frac{5}{2}$ʱ����BCF��������ʱF��$\frac{5}{2}$��$\frac{35}{9}$����
��FG��MN��ʹ��FG=MN������GN����G����ֱ��MN�ĶԳƵ�P������BP��AE��N����ʱ�ı���FMNB���ܳ���̣�
���ɣ�FM+MN+BN+FB=MN+FB+GN+BN=MN+FB+PN+BN��
��������֮���߶���̿�֪��ʱ�ı���FMNB���ܳ���̣�
��֪G��$\frac{7}{2}$��$\frac{26}{9}$����P��-$\frac{35}{9}$��-$\frac{9}{2}$����
��ֱ��BP�Ľ���ʽΪy=$\frac{81}{160}$x-$\frac{81}{32}$��
��$\left\{\begin{array}{l}{y=-x-1}\\{y=\frac{45}{180}x-\frac{45}{32}}\end{array}\right.$$\left\{\begin{array}{l}{y=-x-1}\\{y=\frac{81}{160}x-\frac{81}{32}}\end{array}\right.$���$\left\{\begin{array}{l}{x=\frac{245}{241}}\\{y=-\frac{486}{241}}\end{array}\right.$��
���N���꣨$\frac{245}{241}$��-$\frac{486}{241}$����
�߰ѵ�N����ƽ��1����λ��������ƽ��һ����λ�ɵ�M��
��M��$\frac{4}{241}$��-$\frac{245}{241}$����
��3�����ڣ��������£�
����ͼ2�У���A��D=A��Bʱ����֤��ADA��ա�BA��R������AD=BA�䣬AA��=BR��
��DH��AB��H��
��Rt��ADH����AH=3��DH=4��
��AD=$\sqrt{{3}^{2}+{4}^{2}}$=5��
��BA��=5��A����O�غϣ���
��AA��=1��
��BR=1��
����ͼ3�У���RD=RA��ʱ����RG��AD��G��
��BR=x��DR=RA��=5-x��
��RD=RA�䣬RG��DA�䣬
��DG=GA�䣬
���RA��D=��RDA��=��DAB=��ABD��
��cos��RDG=cos��DAB=$\frac{3}{5}$=$\frac{DG}{DR}$��
��DG=$\frac{3}{5}$��5-x����
��DA��=BA��=$\frac{6}{5}$��5-x����
�ߡ�DAA��ס�BA��R��
��$\frac{DA��}{RA��}$=$\frac{AD}{BA��}$��
��$\frac{\frac{6}{5}��5-x��}{5-x}$=$\frac{5}{\frac{6}{5}��5-x��}$��
��x=$\frac{55}{36}$��
��BR=$\frac{55}{36}$��
�ۡߡ�DRA�䣾��DA��R����DA���DR��
��������������DRA��Ϊ����������ʱBR�ij�Ϊ1��$\frac{55}{36}$��
���� ���⿼����κ����ۺ��⡢һ�κ��������ʡ�����ϵ������������⡢ȫ�������ε��ж������ʡ����������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬ѧ�ṹ�����̽�����⣬�����п�ѹ���⣮

 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�| A�� | 1.42��108 | B�� | 1.42��109 | C�� | 1.42��1010 | D�� | 1.42��1011 |
| A�� | ��-2��4�� | B�� | ��-4��-2�� | C�� | ��4��2�� | D�� | ��-2��-4�� |
| A�� | ����5�� | B�� | ����10�� | C�� | ���� | D�� | ��С��ԭ����$\frac{1}{5}$ |
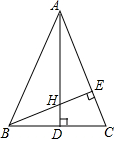 ��ͼ����ABC�У�DE��AD�ֱ���AC��BC���ϵĸ��ߣ��ཻ�ڵ�H����ABE=45�㣬��CBE=��BAD��BD=2$\sqrt{2}$����AH=4$\sqrt{2}$��
��ͼ����ABC�У�DE��AD�ֱ���AC��BC���ϵĸ��ߣ��ཻ�ڵ�H����ABE=45�㣬��CBE=��BAD��BD=2$\sqrt{2}$����AH=4$\sqrt{2}$��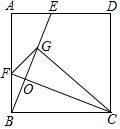 ��ͼ����������ABCD�У�AB=6����E��AD����һ��AE=2������BE����F��AB����һ���㣬����FBC��CF���ۺ�Bǡ������BE�ϵĵ�G����FC��BE�ڵ�O���ֽ���FOG�Ƶ�O��ת�õ���F��OG�䣬����OG�䡢����OF��ֱ�ֱ��AD�ڵ�M��N������OMNΪ����������ʱGM=$\frac{6}{5}$$\sqrt{13}$��
��ͼ����������ABCD�У�AB=6����E��AD����һ��AE=2������BE����F��AB����һ���㣬����FBC��CF���ۺ�Bǡ������BE�ϵĵ�G����FC��BE�ڵ�O���ֽ���FOG�Ƶ�O��ת�õ���F��OG�䣬����OG�䡢����OF��ֱ�ֱ��AD�ڵ�M��N������OMNΪ����������ʱGM=$\frac{6}{5}$$\sqrt{13}$�� ��ͼ��������y=-$\frac{1}{2}$x2+bx+c��ͼ���A��0��1����B��1��3�����㣬��ABΪ����������ABCD����D��x���ϣ����ӳ�BC��x���ڵ�E��
��ͼ��������y=-$\frac{1}{2}$x2+bx+c��ͼ���A��0��1����B��1��3�����㣬��ABΪ����������ABCD����D��x���ϣ����ӳ�BC��x���ڵ�E��