题目内容
12．有6个质地均匀和大小相同的球，每个球只标有一个数字，现将标有3，4，5的三个球放入甲箱中，标有4，5，6的三个球放入乙箱中，小明和小海分别从甲、乙两箱中各摸一球，则小海所摸球上的数字比小明所摸球上数字大的概率为$\frac{2}{3}$．分析 利用列表的方法列举出所有等可能的结果，再找出小海所摸球上的数字比小明所摸球上的数字大的情况数目，两者的比值即为发生得概率．
解答 解：根据题意列表如下：
| 小海 小明 | 4 | 5 | 6 |
| 3 | （3，4） | （3，5） | （3，6） |
| 4 | （4，4） | （4，5） | （4，6） |
| 5 | （5，4） | （5，5） | （5，6） |
因此小海所摸球上的数字比小明所摸球上数字大的概率是$\frac{6}{9}$=$\frac{2}{3}$；
故答案为：$\frac{2}{3}$．
点评 此题考查了利用画树状图及列表格的方法求事件发生的概率，利用了数形结合的思想．通过画树状图或列表法将复杂的概率问题化繁为简，化难为易，因为这种方法可以直观的把所有可能的结果一一罗列出来，方便于计算．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
3．
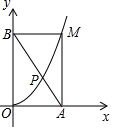如图，点M是抛物线y=ax2（x＞0）上的任意一点，MA⊥x轴于点A，MB⊥y轴于点B，连接AB，交抛物线于点P，则$\frac{PA}{PB}$的值是（ ）
如图，点M是抛物线y=ax2（x＞0）上的任意一点，MA⊥x轴于点A，MB⊥y轴于点B，连接AB，交抛物线于点P，则$\frac{PA}{PB}$的值是（ ）| A． | $\frac{\sqrt{5}-1}{2}$ | B． | $\frac{\sqrt{5}+1}{2}$ | C． | $\frac{3-\sqrt{5}}{2}$ | D． | $\frac{3+\sqrt{5}}{2}$ |
如图是一斜坡的横截面，某人沿着斜坡从P处出发，走了13米到达M处，此时在铅垂方向上上升了5米，那么该斜坡的坡度是5：12．
4．
如图，在矩形ABCD中，AD=$\sqrt{2}$AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：
①∠AED=∠CED；
②OE=OD；
③BH=HF；
④BC-CF=2HE；
⑤AB=HF．
其中正确的有（ ）
如图，在矩形ABCD中，AD=$\sqrt{2}$AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①∠AED=∠CED；
②OE=OD；
③BH=HF；
④BC-CF=2HE；
⑤AB=HF．
其中正确的有（ ）
| A． | ①②③④⑤ | B． | ①②③④ | C． | ①③④⑤ | D． | ①②③⑤ |
如图，矩形ABCD中，AD=10，AB=8，点E为边DC上一动点，连接AE，把△ADE沿AE折叠，使点D落在点D′处，当△DD′C是直角三角形时，DE的长为4或5．
2．
如图，直线b、c被直线a所截，则∠1与∠2是（ ）
如图，直线b、c被直线a所截，则∠1与∠2是（ ）| A． | 同位角 | B． | 同旁内角 | C． | 内错角 | D． | 对顶角 |