题目内容
12.已知直线y=mx与双曲线y=$\frac{k}{x}$的一个交点坐标为(2,4),则它们的另一个交点坐标是( )| A. | (-2,4) | B. | (-4,-2) | C. | (4,2) | D. | (-2,-4) |
分析 反比例函数的图象是中心对称图形,则与经过原点的直线的两个交点一定关于原点对称.
解答 解:∵直线y=mx与双曲线y=$\frac{k}{x}$的一个交点坐标为(2,4),且直线y=mx与双曲线y=$\frac{k}{x}$均关于原点对称.
∴两点关于原点对称,
则另一个交点的坐标为(-2,-4).
故选:D.
点评 本题考查了反比例函数与一次函数的图象的交点、反比例函数图象的中心对称性;熟记关于原点对称是解决问题的关键.

练习册系列答案
相关题目
2.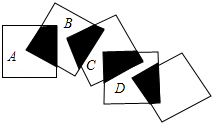 将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
 将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )| A. | 3cm2 | B. | 6cm2 | C. | 9cm2 | D. | 18cm2 |
3.把n边形变为(n+x)边形,内角和增加了720°,则x的值为( )
| A. | 4 | B. | 6 | C. | 5 | D. | 3 |
7.距据2017年镇海区政府工作报告得知,2016年全区生产总值为326.21亿元,年均增长8.8%,增速位居全省前列,将326.21亿元用科学记数法表示为( )
| A. | 326.21×108元 | B. | 3.2521×102元 | C. | 3.2621×1010元 | D. | 0.32621×1011元 |
17.计算(-2)2002+(-2)2001所得的正确结果是( )
| A. | 22001 | B. | -22001 | C. | 1 | D. | 2 |
3.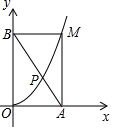 如图,点M是抛物线y=ax2(x>0)上的任意一点,MA⊥x轴于点A,MB⊥y轴于点B,连接AB,交抛物线于点P,则$\frac{PA}{PB}$的值是( )
如图,点M是抛物线y=ax2(x>0)上的任意一点,MA⊥x轴于点A,MB⊥y轴于点B,连接AB,交抛物线于点P,则$\frac{PA}{PB}$的值是( )
 如图,点M是抛物线y=ax2(x>0)上的任意一点,MA⊥x轴于点A,MB⊥y轴于点B,连接AB,交抛物线于点P,则$\frac{PA}{PB}$的值是( )
如图,点M是抛物线y=ax2(x>0)上的任意一点,MA⊥x轴于点A,MB⊥y轴于点B,连接AB,交抛物线于点P,则$\frac{PA}{PB}$的值是( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{3-\sqrt{5}}{2}$ | D. | $\frac{3+\sqrt{5}}{2}$ |